
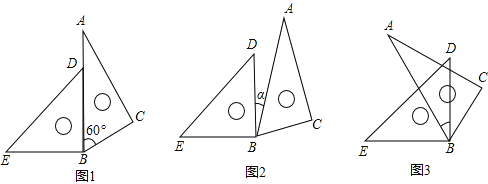
【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
科目:初中数学 来源: 题型:
【题目】如图有A、B、C、D、E五个居民点,每天产生的垃圾量(单位:吨),交通状况和每相邻两个居民点的距离如图所示,现要建一座垃圾中转站(只能建在A、B、C、D、E的其中一处),这五个居民点的垃圾都运到此中转站,那么中转站建在何处,才能使总的运输量最小?(圆圈内的数字为垃圾量,线段上的字母表示距离,b<a<c).中转站应建在 处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,不是互为相反意义的量的是( )
A. 向东走20千米与向西走15千米 B. 收入200元与亏损30元
C. 超过0.05mm与不足0.03mm D. 上升10米和下降7米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
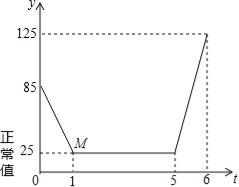
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
查看答案和解析>>
科目:初中数学 来源: 题型:
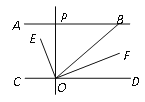
【题目】如下图, AB∥CD, OE平分∠BOC, OF⊥OE, OP⊥CD, ∠ABO=![]() a°, 则下列结论:
a°, 则下列结论:
①∠BOE=![]() (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
其中正确的个数有多少个? --------------( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班7名女生的体重(单位:kg)分别是35、37、38、40、42、42、74,这组数据的众数是( )
A.74 B.44 C.42 D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
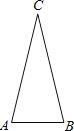
【题目】如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
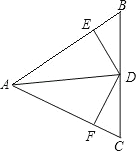
【题目】如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: .
查看答案和解析>>
科目:初中数学 来源: 题型:
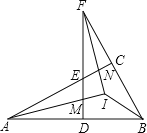
【题目】如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于E、F两点,∠BAC、∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com