
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
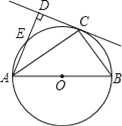
【答案】(1)证明:连结OC(如图所示)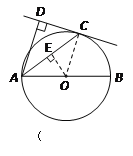
则∠ACO=∠CAO (等腰三角形,两底角相等)
∵CD切⊙O于C,∴CO⊥CD.
又∵AD⊥CD
∴AD∥CO
∴∠DAC=∠ACO (两直线平行,内错角相等)
∴∠DAC=∠CAO
∴AC平分∠BAD ----------------5分
(2)过点E画OE⊥AC于E(如图所示)
在Rt△ADC中,AD=![]() =6
=6
∵OE⊥AC, ∴AE=![]() AC=
AC=![]()
∵ ∠CAO=∠DAC,∠AEO=∠ADC=Rt∠
∴△AEO∽△ADC
∴![]() 即
即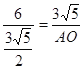
∴AO=![]() 即⊙O的半径为
即⊙O的半径为![]() . ----------------5分
. ----------------5分
【解析】试题分析:(1)首先连接OC,由CD切⊙O于C,根据切线的性质,可得OC⊥CD,又由AD⊥CD,可得OC∥AD,又由OA=OC,易证得∠DAC=∠CAO,即AC平分∠BAD;
(2)首先过点O作OE⊥AC于E,由CD=3,AC=3![]() ,在Rt△ADC中,利用勾股定理即可求得AD的长,由垂径定理,即可得AE的长,然后易证得△AEO∽△ADC,根据相似三角形的对应边成比例,即可求得⊙O的半径长.
,在Rt△ADC中,利用勾股定理即可求得AD的长,由垂径定理,即可得AE的长,然后易证得△AEO∽△ADC,根据相似三角形的对应边成比例,即可求得⊙O的半径长.
试题解析:(1)证明:连接OC,
∵OA=OC,
∴∠ACO=∠CAO,
∵CD切⊙O于C,
∴CO⊥CD.
又∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠BAD;
(2)解:过点O作OE⊥AC于E,

∵CD=3,AC=3![]() ,
,
在Rt△ADC中,AD=![]() ,
,
∵OE⊥AC,
∴AE=![]() AC=
AC=![]() ,
,
∵∠CAO=∠DAC,∠AEO=∠ADC=90°,
∴△AEO∽△ADC,
∴![]() ,
,
即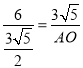 ,
,
∴AO=![]() ,
,
即⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
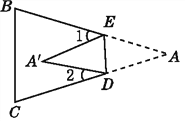
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)?
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
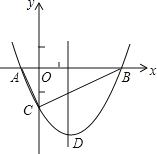
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( ) 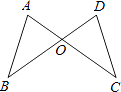
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com