
【题目】已知:二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 当x<1时,y随x的增大而减小
B. 若图象与x轴有交点,则 ![]()
C. 当 a=3时,不等式 ![]() 的解集是
的解集是 ![]()
D. 若将图象向上平移1个单位,再向左平移3个单位后过点 ![]() ,则 a=3
,则 a=3
【答案】B
【解析】
A、当x<1时,在对称轴右侧,由此可以确定y随x的变化情况;B、若图象与x轴有交点,即△=16+4a≥0,利用此即可判断是否正确;C、当a=3时,求出抛物线与x轴的交点坐标,就可求出不等式x2-4x+a<0的解集,然后就可以判断是否正确;D、根据平移规律可以求出a的值,然后判断是否正确.
(1)∵![]()
∴当![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
∴A中说法正确;
( 2)∵由![]() 解得
解得 ![]()
∴B中说法错误;
( 3 )∵当![]() 时,由
时,由 ![]() 解得
解得 ![]() ,
,
∴不等式不等式 ![]() 的解集是
的解集是 ![]()
∴C中说法正确;
( 4 )∵将抛物线![]() 向上平移1个单位,再向左平移3个单位后所得新抛物线的解析式为:
向上平移1个单位,再向左平移3个单位后所得新抛物线的解析式为:![]() 而此时抛物线过点(1,-2),
而此时抛物线过点(1,-2),
∴ ![]() 解得:
解得:![]() ,
,
∴D中说法正确;
故选:B.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画![]() ,使
,使![]() ,
,![]() ,
,![]() 的对边只能在长度分别为
的对边只能在长度分别为![]() 、
、![]() 、
、![]() 、
、![]() 的四条线段中任选,可画出不同形状的三角形的个数是( )(提示:在直角三角形中,如果一个锐角等于
的四条线段中任选,可画出不同形状的三角形的个数是( )(提示:在直角三角形中,如果一个锐角等于![]() ,那么它所对的直角边是斜边的一半)
,那么它所对的直角边是斜边的一半)
A.2个B.3个C.4个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
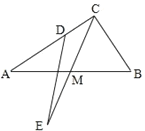
【题目】如图,已知在Rt△ABC中,∠ACB=90°,M是边AB的中点,连接CM并延长到点E,使得EM=![]() AB,D 是边AC上一点,且AD=BC,连接DE.则∠CDE的度数为_______.
AB,D 是边AC上一点,且AD=BC,连接DE.则∠CDE的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E.
(1)求点B的坐标;
(2)连结CE,求线段CE的长;
(3)若点P在线段CB上且OP=![]() ,求P点坐标.
,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
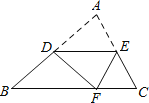
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB⊥BC,AB = BC,E为BC上一点,连接AE,过点C作CF⊥AE,交AE的延长线于点F,连结BF,过点B作BG⊥BF交AE于G.
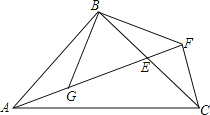
(1)求证:△ABG ≌ △CBF;
(2)若E为BC中点,求证:CF + EF = EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
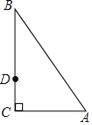
【题目】如图,在△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上的点D处.
(1)用尺规作图的方法,在图中找出点E,F的位置,并连接DE,DF(保留作图痕迹,不要求写作法);
(2)若ED⊥BC,求证:四边形AEDF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com