
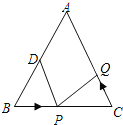
【题目】在△ABC中,AB⊥BC,AB = BC,E为BC上一点,连接AE,过点C作CF⊥AE,交AE的延长线于点F,连结BF,过点B作BG⊥BF交AE于G.
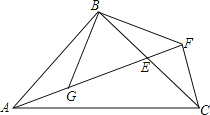
(1)求证:△ABG ≌ △CBF;
(2)若E为BC中点,求证:CF + EF = EG.
【答案】(1)见详解(2)见详解
【解析】
(1)证明∠BAG=∠BCF,∠ABG=∠CBF;即可解决问题.
(2)如图,作辅助线;证明BH=CF,HE=EF;此为解决问题的关键性结论;证明GH=CF,即可解决问题.
解:(1)如图,∵∠ABC=∠AFC=90°,
∴A、B、F、C四点共圆,
∴∠BAG=∠BCF;
∵AB⊥BC,BG⊥BF,
∴∠ABC=∠GBF,
∴∠ABG=∠CBF;
在△ABG与△CBF中,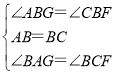 ,
,
∴△ABG≌△CBF(ASA).
(2)
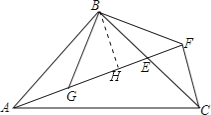
如图,过点B作BH⊥AF;
∵CF⊥AE,
∴BH∥CF,△BHE∽△CFE,
∴BH:CF=GE:EF=BE:CE,
∵BE=CE,
∴BH=CF,HE=EF;
∵△ABG≌△CBF,
∴BG=BF,
∴GH=HF,
∴BH=![]() GF=GH,
GF=GH,
∴GH=CF,而GE=EF,
∴CF+EF=EG.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
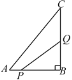
【题目】如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm,若点P从点A沿AB边向B点以1 cm/s的速度移动,点Q从B点沿BC边向点C以2 cm/s的速度移动,两点同时出发.
(1)问几秒后,△PBQ的面积为8cm?
(2)出发几秒后,线段PQ的长为4![]() cm ?
cm ?
(3)△PBQ的面积能否为10 cm2?若能,求出时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 当x<1时,y随x的增大而减小
B. 若图象与x轴有交点,则 ![]()
C. 当 a=3时,不等式 ![]() 的解集是
的解集是 ![]()
D. 若将图象向上平移1个单位,再向左平移3个单位后过点 ![]() ,则 a=3
,则 a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
A.3B.4C.2或 4D.2或3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出△ABC各个顶点的坐标;
(2)判断△ABC的形状;
(3)请在图中画出△ABC关于y轴对称的图形△A'B'C'.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图: △ABC关于![]() 轴对称的图形△
轴对称的图形△![]() ;
;
(2)将点![]() 先向上平移
先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为 ;
的坐标为 ;
(3)△![]() 的面积为 ;
的面积为 ;
(4)若![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]()
![]() ,则△
,则△![]() 周长的最小值为 .
周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com