
【题目】如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
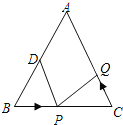
A.3B.4C.2或 4D.2或3
【答案】D
【解析】
分两种情况讨论:
①若△BPD≌△CPQ,根据全等三角形的性质,则BD=CQ=12厘米,BP=CP=![]() BC=
BC=![]() ×16=8(厘米),根据速度、路程、时间的关系即可求得;
×16=8(厘米),根据速度、路程、时间的关系即可求得;
②若△BPD≌△CQP,则CP=BD=12厘米,BP=CQ,得出![]() ,解出即可.
,解出即可.
情况一:
解:∵△ABC中,AB=AC=24厘米,点D为AB的中点,
∴BD=12厘米,
情况一:
若△BPD≌△CPQ,则需BD=CQ=12厘米,BP=CP=![]() BC=
BC=![]() ×16=8(厘米)
×16=8(厘米)
∵点Q的运动速度为2厘米/秒,
∴点Q的运动时间为:8÷2=4(s),
∴v=CQ÷4= 12÷4=3(厘米/秒);
情况二:
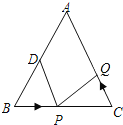
②若△BPD≌△CQP,则CP=BD=12厘米,BP=CQ,
得出![]() ,
,
解得:![]() 解出即可.
解出即可.
因此v的值为:2厘米/秒或3厘米/秒,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,画出函数![]() 的图象,并结合图象回答下列问题:
的图象,并结合图象回答下列问题:
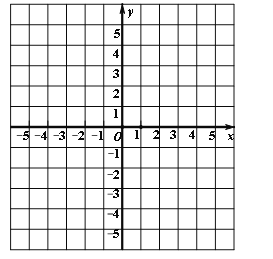
(1)y的值随x值的增大而______(填“增大”或“减小”);
(2)图象与x轴的交点坐标是_____;图象与y轴的交点坐标是______;
(3)当x 时,y <0 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
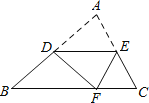
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
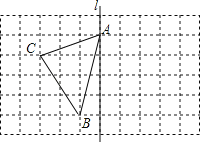
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB⊥BC,AB = BC,E为BC上一点,连接AE,过点C作CF⊥AE,交AE的延长线于点F,连结BF,过点B作BG⊥BF交AE于G.
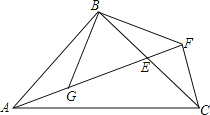
(1)求证:△ABG ≌ △CBF;
(2)若E为BC中点,求证:CF + EF = EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动.
(1)当△ODP是等腰三角形时,请直接写出点P的坐标;
(2)求△ODP周长的最小值.(要有适当的图形和说明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=![]() .求证:CB是⊙O的切线.
.求证:CB是⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com