
【题目】如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列四个判断:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.正确的个数是( )

A.4B.3C.2D.1
【答案】A
【解析】
先由两组对边分别平行的四边形为平行四边形,根据DE∥CA,DF∥BA,得出四边形AEDF是平行四边形,故①正确;当∠BAC=90°,根据推出的平行四边形AEDF,利用有一个角为直角的平行四边形为矩形可得出②正确;如果AD平分∠BAC,通过等量代换可得∠EAD=∠EDA,可得平行四边形AEDF的一组邻边相等,即可得到四边形AEDF是菱形,故③正确;由AD⊥BC且AB=AC,根据等腰三角形的三线合一可得AD平分∠BAC,同理可得四边形AEDF是菱形,故④正确;进而得到正确说法的个数.
解:∵DE∥CA,DF∥BA
∴四边形AEDF是平行四边形,①正确;
若∠BAC=90°
∴平行四边形AEDF为矩形,②正确;
若AD平分∠BAC
∴∠EDA=∠FAD
又DE∥CA,
∴∠EAD=∠EDA,
∴AE=DE.
∴平行四边形AEDF为菱形,③正确;
若AD⊥BC,AB=AC,
∴AD平分∠BAC,
同理可得平行四边形AEDF为菱形,④正确;
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】今年是我国建国70周年,回顾过去展望未来,创新是引领发展的第一动力,北京科技创新能力不断增强,下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况.
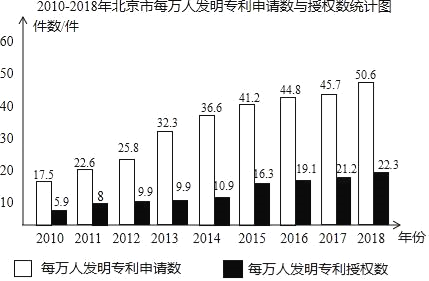
根据统计图提供的信息,下列推断合理的是( )
A. 2010﹣2018年,北京市毎万人发明专利授权数逐年增长
B. 2010﹣2018年,北京市毎万人发明专利授权数的平均数超过10件
C. 2010年申请后得到授权的比例最低
D. 2018年申请后得到授权的比例最高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B→A,B→C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.

(1)若a=4厘米,t=1秒,则PM=______厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
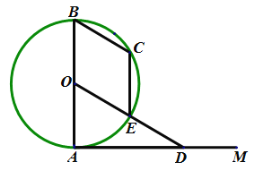
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=1,求⊙O的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com