Question

16．为了解“阳光体育”活动情况，我市教育部门在某所初中2000名学生中，随机抽取了若干学生进行问卷调查（要求每位学生只能填写一种自己喜欢的活动），并将调查的结果绘制成如图的两个不完整的统计图：

根据以上信息解答下列问题：
（1）参加调查的人数共有300人，在扇形图中，表示“C”的扇形的圆心角为108度；
（2）补全条形统计图，并计算扇形统计图中的n；
（3）估计该校喜欢“B”项目的学生一共有多少人？

Answer 1

分析 （1）用喜欢乒乓球的人数除以其所占的百分比即可求得调查的总人数；
（2）用喜欢C项目的人数除以总人数即可求得其百分率，从而得到m的值；
（3）求出喜欢B类项目的占总数的百分比乘总人数即可．

解答 解：（1）观察统计图知喜欢乒乓球的有69人，占总人数的23%，
故调查的总人数有69÷23%=300人，
喜欢跳绳的有300-60-69-36-45=90人，
故C所表示的扇形的圆心角为$\frac{90}{300}$×360°=108°；

（2）m%=$\frac{60}{300}$×100%=20%，故m=20；
统计图如下：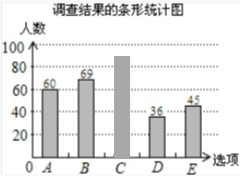


（3）喜欢B项目的有2000×23%=460人．
答：该校喜欢“B”项目的学生一共有460人．

点评 本题考查了条形统计图，解题的关键是仔细的观察两种统计图，并结合两种统计图得到解题的有关信息．