
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2-4ax-5aЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃКy=kx+bгыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=6ACЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2-4ax-5aЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃКy=kx+bгыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=6ACЃЎЗжЮі ЃЈ1ЃЉИљОнХзЮяЯпy=ax2-4ax-5aЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌПЩвдЧѓЕУЕуAКЭЕуBЕФзјБъЃЌгЩОЙ§ЕуAЕФжБЯпlЃКy=kx+bЃЌПЩвдЕУЕНkгыbЕФЙиЯЕЃЌШЛКѓИљОнCD=6ACЃЌПЩвдЧѓЕУkгыaЕФЙиЯЕЃЌДгЖјПЩвдБэЪОГіжБЯпlЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩвджЊЕРЕуAЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮФмГЩЮЊОиаЮЃЌШЛКѓЗжСНжжЧщПіНјааНтД№ЃЌЯШЛГіЯргІЕФЭМаЮЃЌШЛКѓИљОнЬтвтЧѓГіЯргІЕФЕуPЕФзјБъЃЌДгЖјПЩвдНтД№БОЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпХзЮяЯпy=ax2-4ax-5aЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌ
Ёр0=ax2-4ax-5a=aЃЈx-5ЃЉЃЈx+1ЃЉЃЌЕУx1=-1ЃЌx2=5ЃЌ
ЁрЕуAЕФзјБъЪЧЃЈ-1ЃЌ0ЃЉЃЌЕуBЕФзјБъЪЧЃЈ5ЃЌ0ЃЉЃЌ
ЁпОЙ§ЕуAЕФжБЯпlЃКy=kx+bЃЌ
ЁрkЁСЃЈ-1ЃЉ+b=0ЃЌЕУk=bЃЌ
Ёрy=kx+kЃЌ
гжЁпCD=6ACЃЌЕуAЕФзјБъЪЧЃЈ-1ЃЌ0ЃЉЃЌ
ЁрЕуDЕФКсзјБъЮЊ6ЃЌ
Ёр6k+k=aЁС62-4aЁС6-5aЃЌ
НтЕУЃЌk=aЃЌ
ЁржБЯпlЕФКЏЪ§БэДяЪНЪЧy=ax+aЃЌ
МДЕуBЕФзјБъЪЧЃЈ5ЃЌ0ЃЉЃЌжБЯпlЕФКЏЪ§БэДяЪНЪЧy=ax+aЃЛ
ЃЈ2ЃЉЩшPЪЧХзЮяЯпЕФЖдГЦжсЩЯЕФвЛЕуЃЌЕуQдкХзЮяЯпЩЯЃЌвдЕуAЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮФмГЩЮЊОиаЮЃЎ
ЕБADЮЊОиаЮЕФвЛБпЪБЃЌШчЯТЭМ1ЫљЪОЃК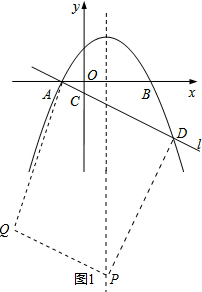
Ёп$\left\{\begin{array}{l}{y=a{x}^{2}-4ax-5a}\\{y=ax+a}\end{array}\right.$
НтЕУЃЌx1=-1ЃЌx2=6
ЁрЕуDЕФзјБъЮЊЃЈ6ЃЌ7aЃЉЃЌ
ЁпХзЮяЯпy=ax2-4ax-5aЕФЖдГЦжсЮЊжБЯпx=$-\frac{-4a}{2a}=2$ЃЌPЪЧХзЮяЯпЕФЖдГЦжсЩЯЕФвЛЕуЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈ2ЃЌmЃЉЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЌЕуQдкХзЮяЯпЩЯЃЌ
ЁрЕуQЕФзјБъЮЊЃЈ-5ЃЌ40aЃЉЃЌ
Ёрm=7a+40a=47aЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ2ЃЌ47aЃЉЃЌ
ЁпADЁЭAQЃЌ
ЁрAD2+AQ2=QD2ЃЌ
МД[6-ЃЈ-1ЃЉ]2+ЃЈ7aЃЉ2+[ЃЈ-1ЃЉ-ЃЈ-5ЃЉ]2+ЃЈ40aЃЉ2=[6-ЃЈ-5ЃЉ]2+ЃЈ7a-40aЃЉ2ЃЌ
НтЕУЃЌ$a=ЁР\frac{\sqrt{10}}{10}$ЃЌ
ЁпaЃМ0ЃЌ
Ёрa=$-\frac{\sqrt{10}}{10}$ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ2ЃЌ$-\frac{47\sqrt{10}}{10}$ЃЉЃЛ
ЕБADЮЊОиаЮЕФЖдНЧЯпЪБЃЌШчЯТЭМ2ЫљЪОЃЌ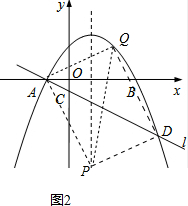
Ёп$\left\{\begin{array}{l}{y=a{x}^{2}-4ax-5a}\\{y=ax+a}\end{array}\right.$
НтЕУx1=-1ЃЌx2=6
ЁрЕуDЕФзјБъЮЊЃЈ6ЃЌ7aЃЉЃЌ
ЁпХзЮяЯпy=ax2-4ax-5aЕФЖдГЦжсЮЊжБЯпx=$-\frac{-4a}{2a}=2$ЃЌPЪЧХзЮяЯпЕФЖдГЦжсЩЯЕФвЛЕуЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈ2ЃЌmЃЉЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЌЕуQдкХзЮяЯпЩЯЃЌ
ЁрЕуQЕФзјБъЮЊЃЈ3ЃЌ-8aЃЉЃЌ
Ёрm=7a-ЃЈ-8aЃЉ=15aЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ2ЃЌ15aЃЉЃЌ
ЁпAQЁЭAPЃЌ
ЁрAQ2+AP2=QP2ЃЌ
МД[3-ЃЈ-1ЃЉ]2+[ЃЈ-8aЃЉ-0]2+[2-ЃЈ-1ЃЉ]2+ЃЈ15a-0ЃЉ2=ЃЈ3-2ЃЉ2+[ЃЈ-8aЃЉ-15a]2ЃЌ
НтЕУa=$ЁР\frac{\sqrt{10}}{10}$ЃЌ
ЁпaЃМ0ЃЌ
Ёрa=-$\frac{\sqrt{10}}{10}$ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ2ЃЌ$-\frac{3\sqrt{10}}{2}$ЃЉЃЎ
гЩЩЯПЩЕУЃЌЕуPЕФзјБъЮЊЃЈ2ЃЌ$-\frac{47\sqrt{10}}{10}$ЃЉЛђЃЈ2ЃЌ$-\frac{3\sqrt{10}}{2}$ЃЉЃЎ
ЕуЦР БОЬтПМВщЖўДЮКЏЪ§злКЯЬтЁЂХзЮяЯпгыxжсЕФНЛЕуЃЌжБЯпгыХзЮяЯпЕФНЛЕуЁЂЙДЙЩЖЈРэЁЂХзЮяЯпЕФЖдГЦжсЃЌНтЬтЕФЙиМќЪЧУїШЗЬтвтЃЌПЩвдЧѓГіЯргІЕФвЛДЮКЏЪ§ЕФБэДяЪНЃЌЛсгУЗжРрЬжТлЕФЪ§бЇЫМЯыЖдЮЪЬтНјааНтД№ЃЌФмЙЛдЫгУЙДЙЩЖЈРэЕФжЊЪЖНјааНтД№ЮЪЬтЃЎ


 аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИ РЖЬьНЬг§ЪюМйгХЛЏбЇЯАЯЕСаД№АИ
РЖЬьНЬг§ЪюМйгХЛЏбЇЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

| ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | |
| АЫЃЈ1ЃЉАр | 75 | 75 | 75 |
| АЫЃЈ2ЃЉАр | 75 | 70 | 90 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌжБОЖABКЭЯвCDЯрНЛЃЌШєЛЁACКЭЛЁBCЕФЖШЪ§БШЪЧ2ЃК1ЃЌDЪЧЛЁABжаЕуЃЌдђЁЯOCDЕФЖШЪ§ЪЧ15ЖШЃЎ
ШчЭМЃЌжБОЖABКЭЯвCDЯрНЛЃЌШєЛЁACКЭЛЁBCЕФЖШЪ§БШЪЧ2ЃК1ЃЌDЪЧЛЁABжаЕуЃЌдђЁЯOCDЕФЖШЪ§ЪЧ15ЖШЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 вбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпABЗжБ№гыxЁЂyжсНЛгкЕуBЁЂAЃЌгыЗДБШР§КЏЪ§ЕФ$y=\frac{k}{x}$ЭМЯѓЗжБ№НЛгкЕуCЁЂDЃЌCEЁЭxжсгкЕуEЃЌ$tanЁЯABO=\frac{1}{2}$ЃЌOB=4ЃЌOE=2ЃЎ
вбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпABЗжБ№гыxЁЂyжсНЛгкЕуBЁЂAЃЌгыЗДБШР§КЏЪ§ЕФ$y=\frac{k}{x}$ЭМЯѓЗжБ№НЛгкЕуCЁЂDЃЌCEЁЭxжсгкЕуEЃЌ$tanЁЯABO=\frac{1}{2}$ЃЌOB=4ЃЌOE=2ЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com