
【题目】为了庆祝中国人民海军成立70周年,某市举行了“海军知识”竞赛,为了了解竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示。请根据图表信息解答下列问题:
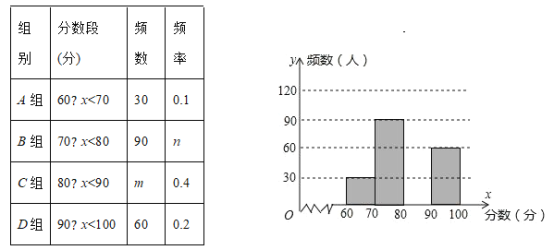
(1)在表中:m=___,n=___;
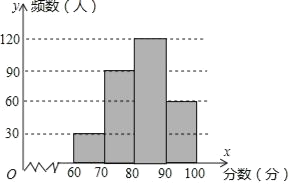
(2)补全频数分布直方图;
(3)若成绩在90分以上(含90分)能获奖,请你估计该是所有参赛的4500名中学生中大约有多少人能获奖.
【答案】(1)120、0.3;(2)详见解析;(3)该市所有参赛的4500名中学生中大约有900人能获奖.
【解析】
(1)先根据A组频数及其频率求得总人数,再根据频率=频数÷总人数可得m、n的值;
(2)根据(1)中所求结果即可补全频数分布直方图;
(3)先求出样本中获奖的百分比,再乘以4500即可求出结果.
(1)∵被调查的总人数为30÷0.1=300,
∴m=300×0.4=120、n=90÷300=0.3,
故答案为:120、0.3
(2)补全频数分布直方图如下:
(3)∵在样本中90![]() 的人数有60人,频率为0.2
的人数有60人,频率为0.2
估计该市总共4500名中学生成绩在90分以上(含90分)的频率是0.2
∴能获奖的中学生大约有4500![]() (人)
(人)
答:该市所有参赛的4500名中学生中大约有900人能获奖.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P(m,n)在抛物线y=ax2-4ax(a>0)上,E为抛物线的顶点.

(1)求点E的坐标(用含a的式子表示);
(2)若点P在第一象限,线段OP交抛物线的对称轴于点C,过抛物线的顶点E作x轴的平行线DE,过点P作x轴的垂线交DE于点D,连接CD,求证:CD∥OE;
(3)如图2,当a=1,且将图1中的抛物线向上平移3个单位,与x轴交于A、B两点,平移后的抛物线的顶点为Q,P是其x轴上方的对称轴上的动点,直线AP交抛物线于另一点D,分别过Q、D作x轴、y轴的平行线交于点E,且∠EPQ=2∠APQ,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0),自变量x与函数y的对应值如下表:

下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2
D. 抛物线的对称轴是直线x=-2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
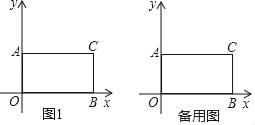
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到△D'CB'(点D'与点D对应).
①若OD=3,求点D'的坐标.
②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板如图所示,叠放在一起.若固定△AOB,将△ACD绕着公共点A按顺时针方向旋转α度(0<α<180).请你探索,当△ACD的一边与△AOB的一边平行时,相应的旋转角α的度数_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
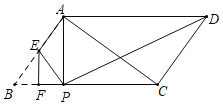
【题目】如图,已知ABCD中,AB=3,BC=5,∠BAC=90°,E、F分别是AB,BC上的动点,EF⊥BC,△BEF与△PEF关于直线EF对称,若△APD是直角三角形,则BF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com