
����Ŀ����ͼ1��P��m��n����������y=ax2-4ax��a��0���ϣ�EΪ�����ߵĶ��㣮

��1�����E�����꣨�ú�a��ʽ�ӱ�ʾ����
��2������P�ڵ�һ���ޣ��߶�OP�������ߵĶԳ����ڵ�C���������ߵĶ���E��x���ƽ����DE������P��x��Ĵ��߽�DE�ڵ�D������CD����֤��CD��OE��
��3����ͼ2����a=1���ҽ�ͼ1�е�����������ƽ��3����λ����x�ύ��A��B���㣬ƽ�ƺ�������ߵĶ���ΪQ��P����x���Ϸ��ĶԳ����ϵĶ��㣬ֱ��AP������������һ��D���ֱ��Q��D��x�ᡢy���ƽ���߽��ڵ�E���ҡ�EPQ=2��APQ�����P�����꣮
���𰸡�(1) E��2����4a����(2)������;(3) P��2��![]() +1����
+1����
��������
��1����ԭʽ��ȡ����ʽȻ�ɽ��
��2����ֱ��OE�Ľ���ʽΪ��y��k x����E�����ɵ�ֱ��OE�Ľ���ʽΪ��y����2ax����P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ���õ�C��2��
���õ�C��2��![]() ����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
��3����a��1ʱ�������߽���ʽΪ��y��x2��4x������ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��Ȼ����P��2��t�����ɵ�AP�Ľ���ʽΪ��y��tx��t��D��3+t��t2+2t����Q��2����1����E��3+t����1��������PE��x����F�����ɽ��
�⣺��1��y��ax2��4ax��a��x2��4x+4��4����a��x��2��2��4a��
��E��2����4a����
��2����ֱ��OE�Ľ���ʽΪ��y��kx��
��E��2����4a������ã�2k����4a��
k����2a��
��ֱ��OE�Ľ���ʽΪ��y����2ax��
��P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ��
��
�൱x��2ʱ��y��![]() ����C��2��
����C��2��![]() ����
����
��D��m����4a����
��ֱ��CD�Ľ���ʽΪ��y��kx+b��
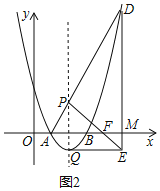
����D��C���������ã�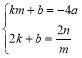 ��n��am2��4am����
��n��am2��4am����
��ã�k����2a��
������ֱ��ϵ����ȣ�
��OE��CD��
��3����ͼ2����a��1ʱ�������߽���ʽΪ��y��x2��4x��
����ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��
��Q��2����1����A��1��0����B��3��0����
��P��2��t����
�ɵ�AP�Ľ���ʽΪ��y��tx��t��
����������Ϊ��![]() ����ã�
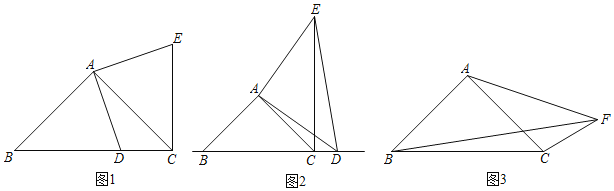
����ã�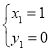 ��
��![]() ��
��
��D��3+t��t2+2t����
��Q��2����1����
��E��3+t����1����
��PQ��QE��t+1��
���EPQ��45�㣬
�ߡ�EPQ��2��APQ��
���APQ��22.5�㣬
��PE��x����F��
�ߡ�DEP��45�㣬
��ME��FM��1��
���FPA����PAF��67.5�㣬
��PF��AF��t+1��
��FP��![]() t��
t��
��![]() t��t+1��
t��t+1��
t��![]() ��
��![]() +1��
+1��
��P��2��![]() +1����
+1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y��mx+n�Ͷ��κ���y��mx2+nx+1������m��0��
��1�������κ���y��mx2+nx+1�����㣨2��0������3��1�����Էֱ�������������Ľ���ʽ��
��2����һ�κ���y��mx+n�����㣨2��0������ͼ����һ�������ޣ����κ���y��mx2+nx+1�����㣨a��y1���ͣ�a+1��y2������y1��y2�������a��ȡֵ��Χ��
��3�������κ���y��mx2+nx+1�Ķ�������ΪA��h��k����h��0����ͬʱ���κ���y��x2+x+1Ҳ����A�㣬��֪��1��h��1�������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ�֣���ͼ1����Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ����߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BD��CE��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤������ͼ2����Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ӳ�����ʱ������EC��д����ʱ�߶�AD��BD��CD֮��ĵ�����ϵ����֤����
��3����չ���٣���ͼ3�����ı���ABCF�У���ABC����ACB����AFC��45�㣮��BF��13��CF��5����ֱ��д��AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��1��������ζԱ���ѧ��������������ϲ���Ŀ������ĵ��飬������������Ϊ�鷨�ͻ滭�ࣨ��ΪA���������ࣨ��ΪB�������ࣨ��ΪC���������ࣨ��ΪD�������ݵ��˽�����ָð�ÿ��ѧ���������˵Ǽ���ÿ��ֻ�Ǽ���һ���Լ���ϲ���Ŀ����������θ��ݵ��������ѧ�������˹��࣬����������������ͳ��ͼ��������ͼ��������Ϣ�������ͬ�⣺
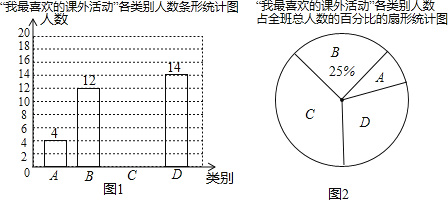
��1�����꼶��1����ѧ��������Ϊ______�ˣ�����ͳ��ͼ��D������Ӧ���ε�Բ�Ľ�Ϊ______�ȣ��벹ȫ����ͳ��ͼ��
��2��ѧУ�������鷨�ͻ滭������ÿ����������ѧ���μӣ�A��4��ѧ����������ѧ���ó��鷨��������ѧ���ó��滭���������ִ�A��4��ѧ���������ȡ����ѧ���μӱ������������б�����״ͼ�ķ�������鵽������ѧ��ǡ����һ���ó��鷨����һ���ó��滭�ĸ��ʣ�
��3�����ȫ����5��������������ôȫ�г������У�ϲ�������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
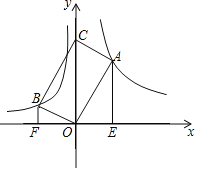
����Ŀ����ͼ����A��B��x����Ϸ�����AOB��90����OA��OB�ֱ��뺯��![]() ��
��![]() ��ͼ����A��B���㣬��OA��OBΪ�ڱ�������AOBC������C��y����ʱ���ֱ����A�͵�B��AE��x�ᣬBF��x�ᣬ����ֱ�ΪE��F����
��ͼ����A��B���㣬��OA��OBΪ�ڱ�������AOBC������C��y����ʱ���ֱ����A�͵�B��AE��x�ᣬBF��x�ᣬ����ֱ�ΪE��F����![]() ��_______��
��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
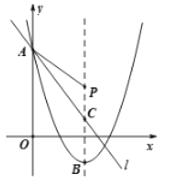
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y=![]() ��y�ύ�ڵ�A������ΪB��ֱ��l��y=-
��y�ύ�ڵ�A������ΪB��ֱ��l��y=-![]() x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+
x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+![]() PC��ֵ��С�����P������Ϊ�� ��
PC��ֵ��С�����P������Ϊ�� ��
A. ��3��1��
B. ��3��![]() ��
��
C. ��3��![]() ��
��
D. ��3��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ף�й���������70���꣬ij�о�����������֪ʶ��������Ϊ���˽⾺���ɼ���������������˲��ֲ���ѧ���ijɼ������������������µ�ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ�������ͼ����Ϣ����������⣺
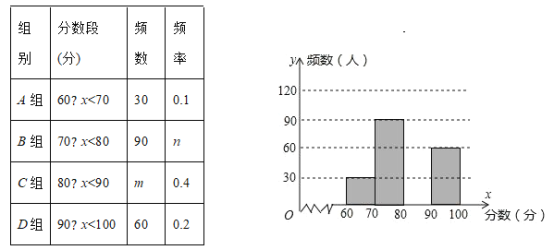
(1)�ڱ��У�m=___��n=___��
(2)��ȫƵ���ֲ�ֱ��ͼ��
(3)���ɼ���90�����ϣ���90�֣��ܻ�������Ƹ������в�����4500����ѧ���д�Լ�ж������ܻ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
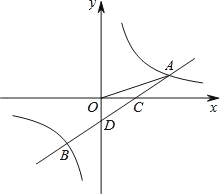
����Ŀ����ͼ��һ�κ���y=ax��1��ͼ���뷴��������y=![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=
��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=![]() ��tan��AOC=
��tan��AOC=![]() ��
��
��1����a��k��ֵ����B�����ꣻ
��2���۲�ͼ����ֱ��д������ʽax��1��![]() �Ľ⼯��
�Ľ⼯��
��3����y���ϴ���һ��P��ʹ����PDC����ODC���ƣ��������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧΪ��չ��У�Ƽ���������ƻ�����A�͡�B�������ͺŵĺ�ģ��������8��A�ͺ�ģ��5��B�ͺ�ģ����2200Ԫ��������4��A�ͺ�ģ��6��B�ͺ�ģ����1520Ԫ����A��B�����ͺź�ģ�ĵ��۷ֱ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com