
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似,且当AC=BC=2时,求AD的长;
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,求AD的长;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.

【答案】(1)![]() ;(2) 1.8或2.5;(3) 当点D是AB的中点时,△CEF与△ABC相似.理由见解析.
;(2) 1.8或2.5;(3) 当点D是AB的中点时,△CEF与△ABC相似.理由见解析.
【解析】
试题(1)△CEF与△ABC相似,又AC=BC=2,可得CE=CF,再证D为AB中点,即可求解;(2)分两种情况:①当△CEF∽△CAB时,此时EF∥AB,证得CD⊥AB,则可利用AD=ACcosA求解;②当△CEF∽CBA时,分别证得AD=CD,CD=BD,则可求得AD=![]() AB=2.5;(3)利用直角三角形中线的性质得CD=DB,则∠DCB=∠B.又可知∠DCB+∠CFE=90°,∠B+∠A=90°,可证得∠CFE=∠A,则可证得△CEF∽△CBA.
AB=2.5;(3)利用直角三角形中线的性质得CD=DB,则∠DCB=∠B.又可知∠DCB+∠CFE=90°,∠B+∠A=90°,可证得∠CFE=∠A,则可证得△CEF∽△CBA.
解:(1)如答图1.∵△CEF∽△ABC,∴![]() =
=![]() ,
,
又∵AC=BC=2,∴CE=CF,
由翻折性质得CE=DE,CF=DF,∴四边形CEDF是菱形,
∴∠ACD=∠BCD,
又∵AC=BC,∴AD=BD=![]() AB=
AB=![]() ×
×![]() =
=![]() .
.
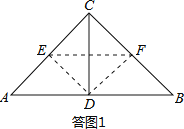
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,有两种情况:
①当△CEF∽△CAB时,如答图2.

此时∠CEF=∠A,∴EF∥BC.
由折叠性质可知,CD⊥EF,∴CD⊥AB,
在Rt△ABC中,AC=3,BC=4,∴AB=5,∴cosA=![]() .
.
∴在Rt△ACD中,AD=ACcosA=3×![]() =1.8;
=1.8;
②当△CEF∽CBA时,如答图3.
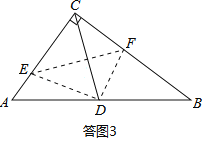
此时∠CEF=∠B.
由折叠性质可知,∠CQE=90°,∴∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,∴AD=CD.
同理可得CD=BD,
∴AD=![]() AB=
AB=![]() ×5=2.5.
×5=2.5.
综上所述,当AC=3,BC=4时,AD的长为1.8或2.5.
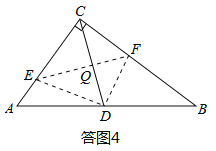
(3)当点D是AB的中点时,△CEF与△ABC相似.理由如下:
如答图4,连接CD,与EF交于点Q.
∵CD是Rt△ABC的中线,∴CD=DB=![]() AB,∴∠DCB=∠B.
AB,∴∠DCB=∠B.
由折叠性质可知,∠CQF=∠DQF=90°,∴∠DCB+∠CFE=90°,
又∵∠B+∠A=90°,∴∠CFE=∠A,
又∵∠ECF=∠BCA,∴△CEF∽△CBA.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线。且点B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,试设明:
(1)BD=DE+CE;
(2)若直线AE绕A点旋转到图2位置(BD<CE),其余条件不变时,则BD与DE、CE的关系如何?
(3)若直线AE绕A点旋转到图3位置(CE<BD),其余条件不变时,则BD与DE、CE的关系 。(直接写出结果)



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,∠A=34°,D,E 分别为 AB,AC 上一点,将△BCD,△ADE 沿 CD,DE 翻折,点 A,B 恰好重合于点 P 处,则∠ACP=_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.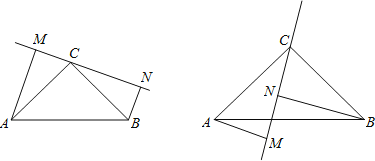
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P,Q分别是边长为4 cm的等边△ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,都以1 cm/s的速度分别向B,C运动.
(1)连接AQ,CP交于点M,则P,Q运动的过程中,∠CMQ的大小变化吗?若变化,说明理由;若不变,求出它的度数;
(2)何时△PBQ是直角三角形?
(3)如图2,若点P,Q在运动到终点后继续在射线 AB,BC上运动,直线AQ,CP交于点M,则∠CMQ的度数为。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com