
【题目】如图,点A(a,a+5)和点B(6,a+1)都在双曲线y=![]() (k<0)上.
(k<0)上.
(1)求k的值;
(2)求△AOB的面积.

【答案】(1)﹣6(2)8
【解析】
(1)由点A、B的坐标利用反比例函数图象上点的坐标特征即可得出关于a的一元二次方程,解之即可得出a值,将其代入k=a(a+5)中即可求出k值;
(2)根据a的值可找出点A、B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式,再根据一次函数图象上点的坐标特征即可找出点C的坐标,根据三角形的面积结合点A、B的横坐标即可求出△AOB的面积.
(1)∵点A(a,a+5)和点B(6,a+1)都在双曲线y=![]() (k<0)上,
(k<0)上,
∴k=a(a+5)=6(a+1),整理得:a2﹣a﹣6=(a+2)(a﹣3)=0,
解得:a=﹣2或a=3(舍去),
∴k=a(a+5)=﹣2×(﹣2+5)=﹣6.
(2)∵a=﹣2,
∴A(﹣2,3),B(6,﹣1).
设直线AB的解析式为y=kx+b(k≠0),
将A(﹣2,3)、B(6,﹣1)代入y=kx+b中,
![]() ,解得:
,解得: ,
,
∴直线AB的解析式为y=﹣![]() x+2.
x+2.
设直线AB与y轴交于点C,则点C的坐标为(0,2),
∴OC=2,
∴S△AOB=![]() OC(xB﹣xA)=
OC(xB﹣xA)=![]() ×2×[6﹣(﹣2)]=8.
×2×[6﹣(﹣2)]=8.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.

(1)求证:△DAC≌△EAB.
(2)求证:CD⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ABC、∠ACB 的角平分线交于点 O,MN 过点 O,且MN∥BC,分别交 AB、AC 于点 M、N.若 MN=5cm,CN=2cm,则 BM=________cm.
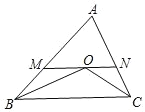
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似,且当AC=BC=2时,求AD的长;
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,求AD的长;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A. 2018 B. 2017 C. 55 D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
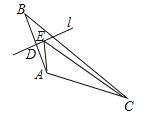
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com