
【题目】下列说法正确的有____.(只填序号)
①边数相等的两个正多边形一定相似;
②已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是20π;
③3是![]() 的平方根;
的平方根;
④若一组数据3,x,4,5,6的众数是3,则中位数是3;
⑤任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
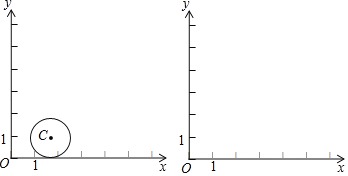
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态环境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
初二:74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整;
整理、描述数据:
成绩x 人数 班级 |
|
|
|
|
|
初一 | 1 | 2 | 3 | 6 | |
初二 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
初一 | 84 | 88.5 | |
初二 | 84.2 | 74 |
(2)得出结论:
你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
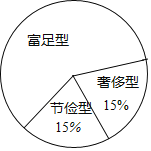
【题目】某校为了解学生每月零用钱情况,从七、八、九年级1200名学生中随机抽取部分学生,对他们今年4月份的零用钱支出情况进行调查统计并绘制成如下统计图表:
组别 | 零用钱支出x(单位:元) | 频数(人数) | 频率 |
节俭型 | x<10 | 2 | 0.05 |
10≤x<20 | 4 | 0.10 | |
富足型 | 20≤x<30 | 12 | |
30≤x<40 | m | ||
奢侈型 | 40≤x<50 | n | |
x≥50 | 2 |
请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n= ;
(2)请估计该校今年4月份零用钱支出在“30≤x<40范围的学生人数;
(3)在抽样的“节俭型”学生中,有2位男生和4位女生,校团委计划从中随机抽取两人参与“映山红”的公益活动,求恰好抽中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.

(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求PAC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
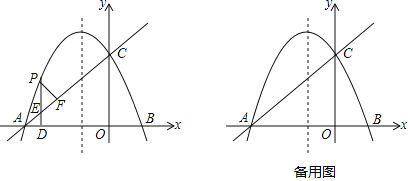
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)以BC为边作正方形CBDE,求对角线BE所在直线的解析式;
(3)点P是抛物线上一点,若∠APB=45°,求出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com