
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
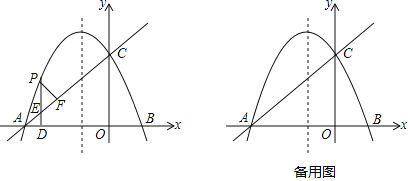
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)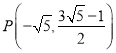 ;(3)存在,Q的坐标为:
;(3)存在,Q的坐标为: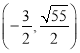 或
或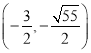
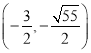 或
或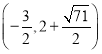 或
或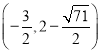 或
或![]() .
.
【解析】
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式,即可求解;
(2)PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2,sin∠EAD=sin∠CAO,
n+2,sin∠EAD=sin∠CAO,![]() ,则AE
,则AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),即可求解;
n+2),即可求解;
(3)等腰三角形分A为顶角顶点、以C为顶角顶点、点Q为顶角顶点,三种情况分别求解即可.
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式得: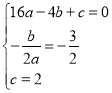 ,解得:
,解得: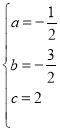 ,故抛物线的表达式为:y
,故抛物线的表达式为:y![]() x2
x2![]() x+2;
x+2;
同理把点A、C坐标代入直线l表达式并解得:y![]() x+2;
x+2;
(2)设P点坐标为(n,![]() n2
n2![]() n+2),∴E点坐标为(n,
n+2),∴E点坐标为(n,![]() n+2),∴PE
n+2),∴PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2.
n+2.
∵A(﹣4,0),C(0,2),OA=4,OC=2,AC=2![]() .
.
∵PD⊥x轴于点D,∴∠ADE=90°,∴sin∠EAD=sin∠CAO,![]() ,∴AE
,∴AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),解得:n=﹣4或
n+2),解得:n=﹣4或![]() (舍去﹣4),∴n=
(舍去﹣4),∴n=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
(3)存在,理由如下:
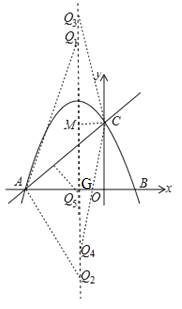
①以A为顶角顶点,AQ=AC,由(2)知AC=2![]() ,若设对称轴与x轴交于点G,则AG
,若设对称轴与x轴交于点G,则AG![]() (﹣4)
(﹣4)![]() ;
;
GQ1=GQ2![]() ,故点Q1、Q2的坐标分别为(
,故点Q1、Q2的坐标分别为(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
②以C为顶角顶点,CQ=CA=2![]() ,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(
,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(![]() ,2),则CM
,2),则CM![]() ,MQ3
,MQ3![]() ,Q3G=2
,Q3G=2![]() ,Q4G=﹣2
,Q4G=﹣2![]() ,故Q3、Q4坐标分别为(
,故Q3、Q4坐标分别为(![]() ,2
,2![]() )、(
)、(![]() ,2
,2![]() );
);
③以点Q为顶角顶点时,同理可得点Q5(![]() ,0);
,0);
故点Q的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
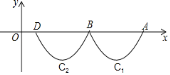
【题目】如图,抛物线![]() 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得到C2,C2与x轴交于点B、D,若直线y=
与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得到C2,C2与x轴交于点B、D,若直线y=![]() x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市精准扶贫工作已进入攻坚阶段.贫困户张伯伯在相关单位的帮扶下把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售在销售的30天中,第一天卖出20千克为了扩大销量采取了降价措施以后每天比前一天多卖出4千克第![]() 天的售价为
天的售价为![]() 元/千克,
元/千克,![]() 关于
关于![]() 的函数解析式为
的函数解析式为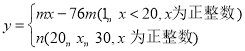 ,且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成本是18元/千克,每天的利润是
,且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成本是18元/千克,每天的利润是![]() 元(利润=销售收入
元(利润=销售收入![]() 成本).
成本).
(1)![]() _____________,
_____________,![]() ____________;
____________;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是半圆O上一个动点,AB为半圆的直径,D是弧BC的中点,过点D作半圆O的切线DE交AC的延长线于点E.
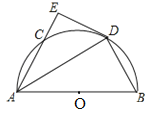
(1)求证:AE⊥DE;
(2)①已知CE=2,DE=4,则AB= ;
②连接OC,DC,当∠BAC= 度时,四边形OBDC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,连接
中,连接![]() 点
点![]() 为
为![]() 上一点,使得
上一点,使得![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
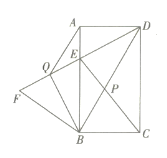
(1)求证:![]() .
.
(2)若![]() 求
求![]() 的长.
的长.
(3)在(2)的条件下,将![]() 沿着
沿着![]() 对折得到
对折得到![]() 点
点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 试求
试求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
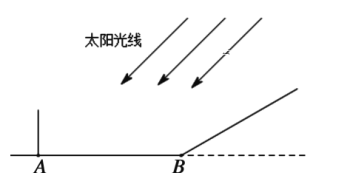
【题目】小芳身高1.6米,此时太阳光线与地面的夹角为45°.
(1)若小芳正站在水平地面A处上时,那么她的影长为多少米?
(2)若小芳来到一个坡度i=![]() 的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
查看答案和解析>>
科目:初中数学 来源: 题型:
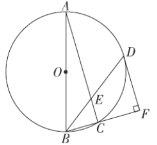
【题目】如图,AB是⊙O的直径,△ABC内接于⊙O.点D在⊙O 上,BD平分∠ABC交AC于点E,DF⊥BC交BC的延长线于点F.
(1)求证:FD是⊙O的切线;
(2)若BD=8,sin∠DBF=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com