
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)以BC为边作正方形CBDE,求对角线BE所在直线的解析式;
(3)点P是抛物线上一点,若∠APB=45°,求出点P的坐标.

【答案】(1)y=![]() x+4;(2)y=﹣3x+24或y=
x+4;(2)y=﹣3x+24或y=![]() ;(3)点P坐标为(﹣4,﹣6)或(10,﹣6).
;(3)点P坐标为(﹣4,﹣6)或(10,﹣6).
【解析】
(1)利用对称轴公式列式即求出a的值,进而得抛物线解析式.
(2)由于边DE所在位置不同,故需对点E所在位置分类讨论.过点E作y轴垂线,根据∠BCE=90°构造模型,即求得点E坐标,进而求直线BE解析式.
(3)由点P运动过程中∠APB=45°联想到圆周上的圆周角,只要构造出∠APB为圆周角,其所对圆心角等于90°即可.故以AB为斜边作等腰直角三角形ABG.若G在第一象限,则圆与抛物线无除A、B外的交点,故点G需在第四象限.求出点G坐标,设P坐标,以PG的长等于半径5![]() 为等量关系列方程,即求得p的值进而得点P坐标.
为等量关系列方程,即求得p的值进而得点P坐标.
解:(1)∵抛物线的对称轴是直线x=3,
∴![]() =3,解得:a=﹣
=3,解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)当y=﹣![]() x2+
x2+![]() x+4=0时,解得:x1=﹣2,x2=8,
x+4=0时,解得:x1=﹣2,x2=8,
∴A(﹣2,0),B(8,0),
∴AB=10,OB=8,
当x=0时,y=﹣![]() x2+
x2+![]() x+4=4,
x+4=4,
∴C(0,4),OC=4,
①如图1,若点E在第一象限,过点E作EF⊥y轴于点F,

∴∠CFE=∠BOC=90°,
∵四边形CBDE是正方形,
∴∠BCE=90°,BC=CE,
∴∠BCO+∠OBC=∠BCO+∠FCE=90°,
∴∠OBC=∠FCE,
在△FCE与△OBC中
 ,
,
∴△FCE≌△OBC(AAS),
∴FC=OB=8,EF=OC=4,
∴OF=OC+FC=12,
∴E(4,12),
设直线BE解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线BE解析式为y=﹣3x+24,
②如图2,若点E在第三象限,过点E作EF⊥y轴于点F,

同理可证:△FCE≌△OBC(AAS),
∴FC=OB=8,EF=OC=4,
∴OF=FC﹣OC=8﹣4=4,
∴E(﹣4,﹣4),
设直线BE解析式为:y=k'x+b',
∴![]() ,解得:
,解得: ,
,
∴直线BE解析式为y=![]() x-
x-![]() ,
,
综上所述,直线BE解析式为y=﹣3x+24或y=![]() x-
x-![]() ;
;
(3)以AB为斜边作等腰Rt△AGB,则AG=BG,∠AGB=90°,
以点G为圆心、AG长为半径画圆,则点P在优弧AB上时总有∠APB=45°,
如图3,若点G在第一象限,⊙G与抛物线交点只有A、B,即没有满足条件的点P使∠APB=45°,

如图4,若点G在第四象限,过点G作GM⊥x轴于点M,
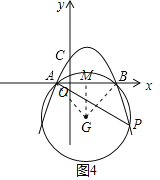
∴AM=BM=GM=![]() AB=5,
AB=5,
∴G(3,﹣5),
设P(p,-![]() p2+
p2+![]() p+4),
p+4),
∵PG=AG=![]() AB=5
AB=5![]() ,
,
∴PG2=50 可得方程:(p﹣3)2+(-![]() p2+
p2+![]() p+4+5)2=50,
p+4+5)2=50,
解得:p1=﹣4,p2=10,p3=﹣2(即点A,舍去),p4=8(即点B,舍去),
∴-![]() p2+
p2+![]() p+4=﹣6,
p+4=﹣6,
∴点P坐标为(﹣4,﹣6)或(10,﹣6).
故答案为:(1)y=![]() x+4;(2)y=﹣3x+24或y=
x+4;(2)y=﹣3x+24或y=![]() ;(3)点P坐标为(﹣4,﹣6)或(10,﹣6).
;(3)点P坐标为(﹣4,﹣6)或(10,﹣6).


科目:初中数学 来源: 题型:
【题目】下列说法正确的有____.(只填序号)
①边数相等的两个正多边形一定相似;
②已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是20π;
③3是![]() 的平方根;
的平方根;
④若一组数据3,x,4,5,6的众数是3,则中位数是3;
⑤任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
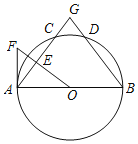
(1)求证:∠F=∠B;
(2)若AB=12,BG=10,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
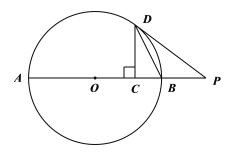
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三上学期期末考试后,数学老师将九年级(1)班的数学成绩制成如图所示的统计图(满分150分,每组含最低分,不含最高分),并给出如下信息:①第二组频率是0.15;②第二、四组的频率和是0.4;③自左至右第三,四,五,六,七组的频数比9:10:7:3:3.请你结合统计图解答下列问题:
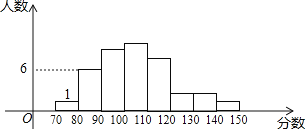
(1)九年级(1)班学生共有____人;
(2)求九年级(1)班在110~120分数段的人数;
(3)如果成绩不少于120分为优秀,那么全年级800人中成绩达到优秀的大约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验.
在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.

根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
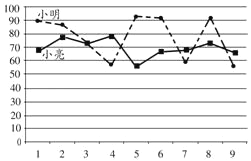
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年南充市有县区申报了长寿之乡,并获认定.上月某中学九(1)班学生社会实践前往该区一乡镇调研进入老龄化社会的数据.按国际通行标准,当一个国家或地区60及60岁以上人口达到人口总数的10%,或65及65岁以上人口达到人口总数的7%,这个区域进入老龄化社会.被调查的800人年龄情况统计图如下:
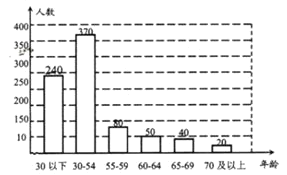
(1)该乡镇是否进入老龄化社会?并说明理由.
(2)请你为该乡镇提一条合理化建议.
(3)在该乡镇60岁及以上人群中随机抽取1人,求年龄不低于70岁的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明利用所学数学知识测量某建筑物BC高度,采用了如下的方法:小明从与某建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为72°,建筑物底端B的俯角为63°,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据小明的测量数据,计算得出建筑物BC的高度约为( )米(计算结果精DE确到0.1米,参考数据:sin72°≈0.95,tan72°≈3.08,sin63°≈0.89,tan63°≈1.96)
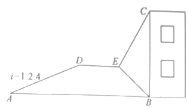
A.157.1 B.157.4 C.257.4 D.257.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com