
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
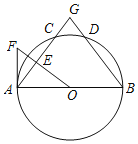
(1)求证:∠F=∠B;
(2)若AB=12,BG=10,求AF的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据圆周角定理得到∠GAB=∠B,根据切线的性质得到∠GAB+∠GAF=90°,证明∠F=∠GAB,等量代换即可证明;
(2)连接OG,根据勾股定理求出OG,证明△FAO∽△BOG,根据相似三角形的性质列出比例式,计算即可.
(1)证明:∵![]() ,
,
∴![]() .
.
∴∠GAB=∠B,
∵AF是⊙O的切线,
∴AF⊥AO.
∴∠GAB+∠GAF=90°.
∵OE⊥AC,
∴∠F+∠GAF=90°.
∴∠F=∠GAB,
∴∠F=∠B;
(2)解:连接OG.
∵∠GAB=∠B,
∴AG=BG.
∵OA=OB=6,
∴OG⊥AB.
∴![]() ,
,
∵∠FAO=∠BOG=90°,∠F=∠B,
∴△FAO∽△BOG,
∴![]() .
.
∴![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态环境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
初二:74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整;
整理、描述数据:
成绩x 人数 班级 |
|
|
|
|
|
初一 | 1 | 2 | 3 | 6 | |
初二 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
初一 | 84 | 88.5 | |
初二 | 84.2 | 74 |
(2)得出结论:
你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.

(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求PAC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
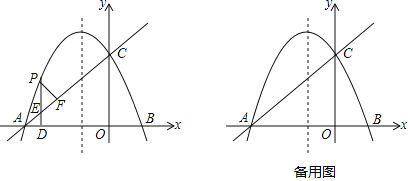
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为2a的正方形ABCD,对角线AC、BD交于点Q,对于平面内的点P与正方形ABCD,给出如下定义:如果![]() ,则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中,若A(﹣1,1),B(﹣1,﹣1),C(1,﹣1),D(1,1).
,则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中,若A(﹣1,1),B(﹣1,﹣1),C(1,﹣1),D(1,1).
(1)在![]() ,
,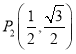 ,
,![]() 中,正方形ABCD的“关联点”有_____;
中,正方形ABCD的“关联点”有_____;
(2)已知点E的横坐标是m,若点E在直线![]() 上,并且E是正方形ABCD的“关联点”,求m的取值范围;
上,并且E是正方形ABCD的“关联点”,求m的取值范围;
(3)若将正方形ABCD沿x轴平移,设该正方形对角线交点Q的横坐标是n,直线![]() 与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”,求n的取值范围.
与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.
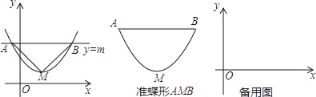
(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)以BC为边作正方形CBDE,求对角线BE所在直线的解析式;
(3)点P是抛物线上一点,若∠APB=45°,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+8与x轴交于A、B两点,交y轴于点C,连接BC,且点D坐标为(﹣2,4),tan∠OBC=![]() .
.
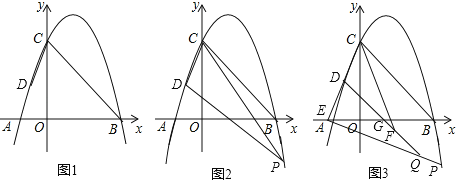
(1)求抛物线的解析式;
(2)P为第四象限抛物线上一点,连接PC、PD,设点P的横坐标为t,△PCD的面积为S,求S与t的函数关系式;
(3)延长CD交x轴于点E,连接PE,直线DG与x轴交于点G,与PE交于点Q,且OG=2,点F在DQ上,∠DQE+∠BCF=45°,若FQ=2![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com