
【题目】如图,抛物线y=ax2+bx+8与x轴交于A、B两点,交y轴于点C,连接BC,且点D坐标为(﹣2,4),tan∠OBC=![]() .
.
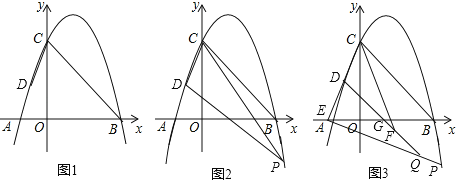
(1)求抛物线的解析式;
(2)P为第四象限抛物线上一点,连接PC、PD,设点P的横坐标为t,△PCD的面积为S,求S与t的函数关系式;
(3)延长CD交x轴于点E,连接PE,直线DG与x轴交于点G,与PE交于点Q,且OG=2,点F在DQ上,∠DQE+∠BCF=45°,若FQ=2![]() ,求点P的坐标.
,求点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+8;(2)S=
x+8;(2)S=![]() t2+
t2+![]() t,(3)P(
t,(3)P(![]() ,
,![]() ).
).
【解析】
(1)在Rt△OBC中,tan∠OBC=![]() =
=![]() ,则OB=6,即可求解;
,则OB=6,即可求解;
(2)S=S△PMD﹣S△PMC=![]() PM(xP﹣xD﹣xP)即可求解;
PM(xP﹣xD﹣xP)即可求解;
(3)证明FC是∠OCB角平分线,求出点V(![]() ,0),点F(3,﹣1)、点Q(5,﹣3),即可求解.
,0),点F(3,﹣1)、点Q(5,﹣3),即可求解.
(1)在Rt△OBC中,tan∠OBC=![]() =
=![]() ,∴OB=6,
,∴OB=6,
∴点B(6,0),
∴![]() ,解得:
,解得: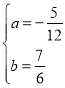 ,
,
故抛物线的表达式为:y=![]() x2+
x2+![]() x+8…①;
x+8…①;
(2)过点P作PM∥y轴交CD延长线于点M,
将D、C的坐标代入一次函数表达式并解得:
直线DC的表达式为:y=2x+8,
则点E(﹣4,0),
设点M(t,2t+8),
则PM=2t+8﹣(![]() t2+
t2+![]() t+8)=
t+8)=![]() t2+
t2+![]() t,
t,
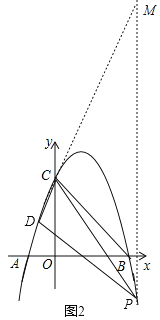
S=S△PMD﹣S△PMC=![]() PM(xP﹣xD﹣xP)=
PM(xP﹣xD﹣xP)=![]() ×2(
×2(![]() t2+
t2+![]() t)=
t)=![]() t2+
t2+![]() t,
t,
(3)将点G(2,0)、点D坐标代入一次函数表达式并解得:
直线DG的表达式为:y=﹣x+2…②,
∴∠DGA=45°,
过点F作FK⊥y轴于点K,过点Q作QL⊥FK于点L交x轴于点S,直线CF交x轴于点V,
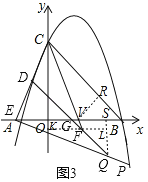
∴∠FQL=∠LFQ=45°,∴FL=QL=![]() FQ=2,
FQ=2,
设点F(m,﹣m+2),则点Q(m+2,﹣m),
tan∠FCK=![]() =
=![]() ,tan∠QEB=
,tan∠QEB=![]() =
=![]() ,
,
∴∠FCK=∠QEB,
∵∠QEB+∠BCF=45°,∠DQE+∠QEB=45°,
∴∠QEB=∠BCF,∠FCK=∠BCF,
过点V作VR⊥BC于点R,设OV=n,
则VB=6﹣n,CO=CR=8,则BR=2,
则(6﹣n)2=n2+4,解得:n=![]() ,则点V(
,则点V(![]() ,0),
,0),
将直线C(0,8)、V(![]() ,0)坐标代入一次函数表达式并解得:
,0)坐标代入一次函数表达式并解得:
直线CV(CF)的表达式为:y=﹣3x+8…③,
联立②③并解得:x=3,则点F(3,﹣1),
而FQ=2![]() ,在等腰直角三角形FQL中,
,在等腰直角三角形FQL中,
FL=QL=2![]() ×
×![]() =2,
=2,
故点Q(5,﹣3),点E(﹣4,0),
同理可得直线EQ的表达式为:y=![]() x﹣
x﹣![]() …④,
…④,
联立①④并解得:x=![]() (舍去负值),
(舍去负值),
∴P(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
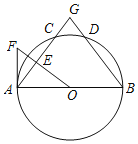
(1)求证:∠F=∠B;
(2)若AB=12,BG=10,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
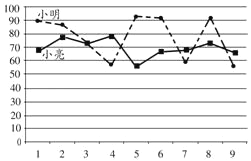
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年南充市有县区申报了长寿之乡,并获认定.上月某中学九(1)班学生社会实践前往该区一乡镇调研进入老龄化社会的数据.按国际通行标准,当一个国家或地区60及60岁以上人口达到人口总数的10%,或65及65岁以上人口达到人口总数的7%,这个区域进入老龄化社会.被调查的800人年龄情况统计图如下:
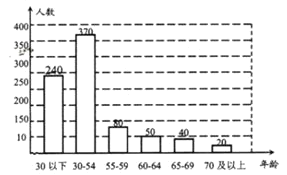
(1)该乡镇是否进入老龄化社会?并说明理由.
(2)请你为该乡镇提一条合理化建议.
(3)在该乡镇60岁及以上人群中随机抽取1人,求年龄不低于70岁的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上
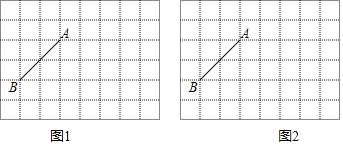
(1)在图1中画一个以线段AB为一边的矩形,点C、D均在小正方形的顶点上,且矩形ABCD的面积为4;
(2)在图2中画一个三角形△ABE,点E在小正方形的顶点上,且△ABE的面积为2,且∠AEB的正切值为![]() ,请直接写出BE的长.
,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() .分别以
.分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.点
轴,建立如图所示的平面直角坐标系.点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 的反比例函数
的反比例函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() .
.
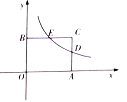
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)问在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的值最小,若存在,请求出点
的值最小,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
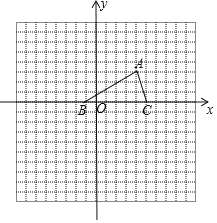
【题目】如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(﹣1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,则点C的对应点C1的坐标为 ;(不用画图)
(2)在图中画出将△ABC绕点B逆时针旋转90°得到的△A′BC′;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使S△ABC:S![]() =1:4,在图中画出△AB2C2.
=1:4,在图中画出△AB2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
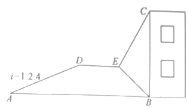
【题目】如图,小明利用所学数学知识测量某建筑物BC高度,采用了如下的方法:小明从与某建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为72°,建筑物底端B的俯角为63°,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据小明的测量数据,计算得出建筑物BC的高度约为( )米(计算结果精DE确到0.1米,参考数据:sin72°≈0.95,tan72°≈3.08,sin63°≈0.89,tan63°≈1.96)
A.157.1 B.157.4 C.257.4 D.257.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
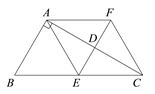
(1)求证:四边形AECF是菱形;
(2)若AB=10,∠ACB=30°,求菱形AECF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com