
ЁОЬтФПЁПГѕШ§ЩЯбЇЦкЦкФЉПМЪдКѓЃЌЪ§бЇРЯЪІНЋОХФъМЖЃЈ1ЃЉАрЕФЪ§бЇГЩМЈжЦГЩШчЭМЫљЪОЕФЭГМЦЭМЃЈТњЗж150ЗжЃЌУПзщКЌзюЕЭЗжЃЌВЛКЌзюИпЗжЃЉЃЌВЂИјГіШчЯТаХЯЂЃКЂйЕкЖўзщЦЕТЪЪЧ0.15ЃЛЂкЕкЖўЁЂЫФзщЕФЦЕТЪКЭЪЧ0.4ЃЛЂлздзѓжСгвЕкШ§ЃЌЫФЃЌЮхЃЌСљЃЌЦпзщЕФЦЕЪ§БШ9ЃК10ЃК7ЃК3ЃК3ЃЎЧыФуНсКЯЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
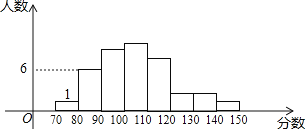
ЃЈ1ЃЉОХФъМЖЃЈ1ЃЉАрбЇЩњЙВга____ШЫЃЛ
ЃЈ2ЃЉЧѓОХФъМЖЃЈ1ЃЉАрдк110~120ЗжЪ§ЖЮЕФШЫЪ§ЃЛ
ЃЈ3ЃЉШчЙћГЩМЈВЛЩйгк120ЗжЮЊгХауЃЌФЧУДШЋФъМЖ800ШЫжаГЩМЈДяЕНгХауЕФДѓдМЖрЩйШЫЃП
ЁОД№АИЁПЃЈ1ЃЉ40ЃЛЃЈ2ЃЉ7ЃЛЃЈ3ЃЉ140.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕкЖўзщЦЕЪ§МАЦфЦЕТЪПЩЕУзмШЫЪ§ЃЛ
ЃЈ2ЃЉЯШгЩЖўЁЂЫФзщЕФЦЕТЪКЭЧѓЕУЖдгІЦЕЪ§КЭЃЌДгЖјЧѓЕУЕкЫФзщЦЕЪ§ЃЌдйгЩздзѓжСгвЕкШ§ЃЌЫФЃЌЮхЃЌСљЃЌЦпзщЕФЦЕЪ§БШ9ЃК10ЃК7ЃК3ЃК3ЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉИљОнЦЕЪ§КЭЮЊзмЪ§ЧѓЕУзюКѓвЛзщЦЕЪ§ЃЌгУзмШЫЪ§ГЫвдбљБОжаКѓШ§зщШЫЪ§КЭЫљеМБШР§МДПЩЕУЃЎ
НтЃКЃЈ1ЃЉЁпЕкЖўзщЦЕТЪЪЧ0.15ЃЌЕкЖўзщЕФЦЕЪ§ЮЊ6ЃЌ
ЁрОХФъвЛАрбЇЩњЙВгаЃК6ЁТ0.15ЃН40ЃЈШЫЃЉЃЛ
ЃЈ2ЃЉЁпЂйЕкЖўзщЦЕТЪЪЧ0.15ЃЛЂкЕкЖўЁЂЫФзщЕФЦЕТЪКЭЪЧ0.4ЃЛ
ЁрЕкЫФзщЦЕТЪЪЧ0.25ЃЌ
ЁрЕкЫФзщЦЕЪ§ЪЧЃК40ЁС0.25ЃН10ЃЌ
ЁпздзѓжСгвЕкШ§ЃЌЫФЃЌЮхЃЌСљЃЌЦпзщЕФЦЕЪ§БШ9ЃК10ЃК7ЃК3ЃК3ЃЌ
ЁрОХФъвЛАрдк110Љ120ЗжЪ§ЖЮЕФШЫЪ§ЮЊЃК7ЃЎ
ЃЈ3ЃЉЁпЕкШ§ЃЌЫФЃЌЮхЃЌСљЃЌЦпзщЕФЦЕЪ§БШ9ЃК10ЃК7ЃК3ЃК3ЃЌЕкЫФзщЦЕЪ§ЪЧ10ЃЌ
ЁрЕкШ§ЃЌЫФЃЌЮхЃЌСљЃЌЦпзщЕФЦЕЪ§ЗжБ№ЮЊЃК9ЃЌ10ЃЌ7ЃЌ3ЃЌ3ЃЌ
ЁпЕквЛЁЂЖўзщЕФЦЕЪ§ЗжБ№ЮЊЃК1ЃЌ6ЃЌ
ЁрЕкАЫзщЕФЦЕЪ§ЮЊЃК40Љ1Љ6Љ9Љ10Љ7Љ3Љ3ЃН1ЃЌ
ЁрГЩМЈВЛЩйгк120ЗжЕФгаЃК3+3+1ЃН7ЃЈШЫЃЉЃЌ
ЁрШЋФъМЖ800ШЫжаГЩМЈДяЕНгХауЕФДѓдМЃК800ЁС![]() ЃН140ЃЈШЫЃЉЃЎ
ЃН140ЃЈШЫЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ1ЃЉ40ЃЛЃЈ2ЃЉ7ЃЛЃЈ3ЃЉ140.


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњУПдТСугУЧЎЧщПіЃЌДгЦпЁЂАЫЁЂОХФъМЖ1200УћбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњЃЌЖдЫћУЧНёФъ4дТЗнЕФСугУЧЎжЇГіЧщПіНјааЕїВщЭГМЦВЂЛцжЦГЩШчЯТЭГМЦЭМБэЃК
зщБ№ | СугУЧЎжЇГіxЃЈЕЅЮЛЃКдЊЃЉ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
НкМѓаЭ | xЃМ10 | 2 | 0.05 |
10ЁмxЃМ20 | 4 | 0.10 | |
ИЛзуаЭ | 20ЁмxЃМ30 | 12 | |
30ЁмxЃМ40 | m | ||
ЩнГоаЭ | 40ЁмxЃМ50 | n | |
xЁн50 | 2 |
ЧыИљОнЭМБэжаЫљИјЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкетДЮЕїВщжаЙВЫцЛњГщШЁСЫЁЁ ЁЁУћбЇЩњЃЌЭМБэжаЕФmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыЙРМЦИУаЃНёФъ4дТЗнСугУЧЎжЇГідкЁА30ЁмxЃМ40ЗЖЮЇЕФбЇЩњШЫЪ§ЃЛ
ЃЈ3ЃЉдкГщбљЕФЁАНкМѓаЭЁБбЇЩњжаЃЌга2ЮЛФаЩњКЭ4ЮЛХЎЩњЃЌаЃЭХЮЏМЦЛЎДгжаЫцЛњГщШЁСНШЫВЮгыЁАгГЩНКьЁБЕФЙЋвцЛюЖЏЃЌЧѓЧЁКУГщжавЛФавЛХЎЕФИХТЪЃЎ
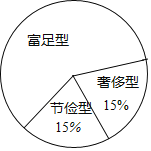
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊБпГЄЮЊ2aЕФе§ЗНаЮABCDЃЌЖдНЧЯпACЁЂBDНЛгкЕуQЃЌЖдгкЦНУцФкЕФЕуPгые§ЗНаЮABCDЃЌИјГіШчЯТЖЈвхЃКШчЙћ![]() ЃЌдђГЦЕуPЮЊе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБ.дкЦНУцжБНЧзјБъЯЕxOyжаЃЌШєAЃЈЉ1ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌЉ1ЃЉЃЌCЃЈ1ЃЌЉ1ЃЉЃЌDЃЈ1ЃЌ1ЃЉ.
ЃЌдђГЦЕуPЮЊе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБ.дкЦНУцжБНЧзјБъЯЕxOyжаЃЌШєAЃЈЉ1ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌЉ1ЃЉЃЌCЃЈ1ЃЌЉ1ЃЉЃЌDЃЈ1ЃЌ1ЃЉ.
ЃЈ1ЃЉдк![]() ЃЌ
ЃЌ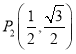 ЃЌ
ЃЌ![]() жаЃЌе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБга_____ЃЛ
жаЃЌе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБга_____ЃЛ
ЃЈ2ЃЉвбжЊЕуEЕФКсзјБъЪЧmЃЌШєЕуEдкжБЯп![]() ЩЯЃЌВЂЧвEЪЧе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЩЯЃЌВЂЧвEЪЧе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєНЋе§ЗНаЮABCDбиxжсЦНвЦЃЌЩшИУе§ЗНаЮЖдНЧЯпНЛЕуQЕФКсзјБъЪЧnЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№ЯрНЛгкMЁЂNСНЕу.ШчЙћЯпЖЮMNЩЯЕФУПвЛИіЕуЖМЪЧе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБЃЌЧѓnЕФШЁжЕЗЖЮЇ.
гыxжсЁЂyжсЗжБ№ЯрНЛгкMЁЂNСНЕу.ШчЙћЯпЖЮMNЩЯЕФУПвЛИіЕуЖМЪЧе§ЗНаЮABCDЕФЁАЙиСЊЕуЁБЃЌЧѓnЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгкxжсЕФНЛЕузјБъЗжБ№ЮЊЃЈx1ЃЌ0ЃЉЃЌЃЈx2ЃЌ0ЃЉЃЌЧвx1ЃМx2ЃЌЭМЯѓЩЯгавЛЕуMЃЈx0ЃЌy0ЃЉдкxжсЯТЗНЃЌЖдгквдЯТЫЕЗЈЃКЂйb2Љ4acЃО0ЂкxЃНx0ЪЧЗНГЬax2+bx+cЃНy0ЕФНтЂлx1ЃМx0ЃМx2ЂмaЃЈx0Љx1ЃЉЃЈx0Љx2ЃЉЃМ0Цфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.ЂйЂлЂмB.ЂйЂкЂмC.ЂйЂкЂлD.ЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЪЧ3ЃЌбгГЄABжСЕуPЁЂбгГЄBCжСЕуQЃЌЪЙBPЃНCQЃЌСЌНгAQЃЌDPНЛгкЕуOЃЌЯрQНЛCDгкЕуFЃЌDPНЛBCгкЕуEЃЌСЌНгAEЃЎ
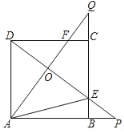
ЃЈ1ЃЉЧѓжЄЃКAQЁЭDPЃЛ
ЃЈ2ЃЉЧѓжЄЃКSЁїAODЃНSЫФБпаЮOECFЃЛ
ЃЈ3ЃЉЕБBPЃН1ЪБЃЌЧыжБНгаДГіOEЃКOAЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНax2+![]() x+4ЕФЖдГЦжсЪЧжБЯпxЃН3ЃЌЧвгыxжсНЛгкAЁЂBСНЕуЃЈЕуBдкЕуAЕФгвВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
x+4ЕФЖдГЦжсЪЧжБЯпxЃН3ЃЌЧвгыxжсНЛгкAЁЂBСНЕуЃЈЕуBдкЕуAЕФгвВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвдBCЮЊБпзїе§ЗНаЮCBDEЃЌЧѓЖдНЧЯпBEЫљдкжБЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕуPЪЧХзЮяЯпЩЯвЛЕуЃЌШєЁЯAPBЃН45ЁуЃЌЧѓГіЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
дкЪ§бЇПЮЩЯЃЌРЯЪІЬсГіШчЯТЮЪЬтЃК

ГпЙцзїЭМЃК
вбжЊЃКЯпЖЮaЃЌbЃЎ
ЧѓзїЃКЕШбќЁїABCЃЌЪЙABЃНACЃЌBCЃНaЃЌBCБпЩЯЕФИпЮЊbЃЎ
аЁЬЮЕФзїЭМВНжшШчЯТЃК
ШчЭМ
ЃЈ1ЃЉзїЯпЖЮBCЃНaЃЛ
ЃЈ2ЃЉзїЯпЖЮBCЕФДЙжБЦНЗжЯпMNНЛЯпЖЮBC
гкЕуDЃЛ
ЃЈ3ЃЉдкMNЩЯНиШЁЯпЖЮDAЃНbЃЌСЌНгABЃЌACЃЎ
ЫљвдЁїABCМДЮЊЫљЧѓзїЕФЕШбќШ§НЧаЮЃЎ
РЯЪІЫЕЃКЁАаЁЬЮЕФзїЭМВНжше§ШЗЁБЃЎ
ЧыЛиД№ЃКЕУЕНЁїABCЪЧЕШбќШ§НЧаЮЕФвРОнЪЧЃК
Ђй_____ЃЛ
Ђк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
Ъ§бЇПЮЩЯРЯЪІВМжУвЛЕРзїЭМЬтЃК
вбжЊЃКжБЯпlКЭlЭтвЛЕуPЃЎ
ЧѓзїЃКЙ§ЕуPЕФжБЯпmЃЌЪЙЕУmЁЮlЃЎ
аЁЖЋЕФзїЗЈШчЯТЃК
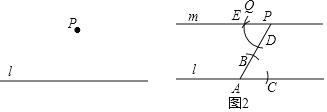
зїЗЈЃКШчЭМ2ЃЌ
ЃЈ1ЃЉдкжБЯпlЩЯШЮШЁЕуAЃЌСЌНгPAЃЛ
ЃЈ2ЃЉвдЕуAЮЊAаФЃЌЪЪЕБГЄЮЊАыОЖзїЛЁЃЌЗжБ№НЛЯпЖЮPAгкЕуBЃЌжБЯпlгкЕуCЃЛ
ЃЈ3ЃЉвдЕуPЮЊдВаФЃЌABГЄЮЊАыОЖзїЛЁDQЃЌНЛЯпЖЮPAгкЕуDЃЛ
ЃЈ4ЃЉвдЕуDЮЊдВаФЃЌBCГЄЮЊАыОЖзїЛЁЃЌНЛЛЁDQгкЕуEЃЌзїжБЯпPEЃЎЫљвджБЯпPEОЭЪЧЫљЧѓзїЕФжБЯпmЃЎ
РЯЪІЫЕЃКЁАаЁЖЋЕФзїЗЈЪЧе§ШЗЕФЃЎЁБ
ЧыЛиД№ЃКаЁЖЋЕФзїЭМвРОнЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕРЯЪІЖдЪдОэНВЦРПЮжаОХФъМЖбЇЩњВЮгыЕФЩюЖШгыЙуЖШНјааЦРМлЕїВщЃЌУПЮЛбЇЩњзюжеЦРМлНсЙћЮЊжїЖЏжЪвЩЁЂЖРСЂЫМПМЁЂзЈзЂЬ§НВЁЂНВНтЬтФПЫФЯюжаЕФвЛЯюЃЎЦРМлзщЫцЛњГщШЁСЫШєИЩУћГѕжабЇЩњЕФВЮгыЧщПіЃЌЛцжЦГЩШчЭМЫљЪОЕФЦЕЪ§ЗжВМжБЗНЭМКЭЩШаЮЭГМЦЭМЃЈОљВЛЭъећЃЉЃЌЧыИљОнЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК


ЃЈ1ЃЉдкетДЮЦРМлжаЃЌвЛЙВГщВщСЫУћбЇЩњЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЯюФПЁАжїЖЏжЪвЩЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊЖШЃЛ
ЃЈ3ЃЉЧыНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ4ЃЉШчЙћШЋЪаОХФъМЖбЇЩњга8000УћЃЌФЧУДдкЪдОэЦРНВПЮжаЃЌЁАЖРСЂЫМПМЁБЕФОХФъМЖбЇЩњдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com