
【题目】阅读下列材料:
数学课上老师布置一道作图题:
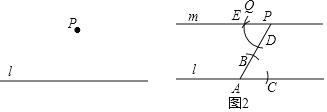
已知:直线l和l外一点P.
求作:过点P的直线m,使得m∥l.
小东的作法如下:
作法:如图2,
(1)在直线l上任取点A,连接PA;
(2)以点A为圓心,适当长为半径作弧,分别交线段PA于点B,直线l于点C;
(3)以点P为圆心,AB长为半径作弧DQ,交线段PA于点D;
(4)以点D为圆心,BC长为半径作弧,交弧DQ于点E,作直线PE.所以直线PE就是所求作的直线m.
老师说:“小东的作法是正确的.”
请回答:小东的作图依据是________.
 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究方程x3﹣x﹣2=0的实数根的个数.
小芳想起了曾经解决的一个问题:通过函数图象探究方程x2+3x﹣1=0的实数根的个数,她想到了如下的几个方法:
方法1:方程x2+3x﹣1=0的根可以看作是抛物线y=x2+3x﹣1与直线y=0(即x轴)交点的横坐标;这两个图象的交点个数即是方程x2+3x﹣1=0的实数根的个数.
方法2:将方程变形成x2=﹣3x+1,那么方程x2+3x﹣1=0的根也可以看作是抛物线y=x2与直线y=﹣3x+1交点的横坐标;这两个图象的交点个数即是方程x2+3x﹣1=0的实数根的个数.
方法3:由于x≠0,将方程变形成![]() ,那么方程x2+3x﹣1=0的根也可以看作是直线y=x+3与双曲线
,那么方程x2+3x﹣1=0的根也可以看作是直线y=x+3与双曲线![]() 交点的横坐标;这两个图象的交点个数即是方程x2+3x﹣1=0的实数根的个数.
交点的横坐标;这两个图象的交点个数即是方程x2+3x﹣1=0的实数根的个数.
她类比上述方法,借助函数图象的交点个数对方程x3﹣x﹣2=0的实数根的个数进行了探究.
下面是小芳的探究过程,请补充完成:
(1)x=0 方程x3﹣x﹣2=0的根;(填”是”或”不是”)
(2)方程x3﹣x﹣2=0的根可以看作是函数 与函数 的图象交点的横坐标;
(3)在同一坐标系中画出两个函数的图象;
(4)观察图象可得,方程x3﹣x﹣2=0的实数根的个数是 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三上学期期末考试后,数学老师将九年级(1)班的数学成绩制成如图所示的统计图(满分150分,每组含最低分,不含最高分),并给出如下信息:①第二组频率是0.15;②第二、四组的频率和是0.4;③自左至右第三,四,五,六,七组的频数比9:10:7:3:3.请你结合统计图解答下列问题:
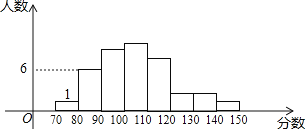
(1)九年级(1)班学生共有____人;
(2)求九年级(1)班在110~120分数段的人数;
(3)如果成绩不少于120分为优秀,那么全年级800人中成绩达到优秀的大约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
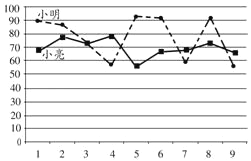
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
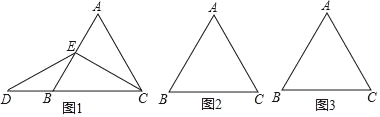
【题目】在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.
(1)如图1,AB=1,点E是AB的中点,求BD的长;
(2)点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;
(3)点E不在线段AB上,请在图3中画出符合条件的一个图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年南充市有县区申报了长寿之乡,并获认定.上月某中学九(1)班学生社会实践前往该区一乡镇调研进入老龄化社会的数据.按国际通行标准,当一个国家或地区60及60岁以上人口达到人口总数的10%,或65及65岁以上人口达到人口总数的7%,这个区域进入老龄化社会.被调查的800人年龄情况统计图如下:
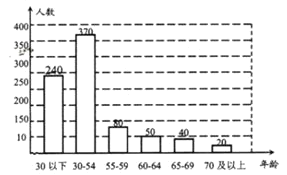
(1)该乡镇是否进入老龄化社会?并说明理由.
(2)请你为该乡镇提一条合理化建议.
(3)在该乡镇60岁及以上人群中随机抽取1人,求年龄不低于70岁的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上
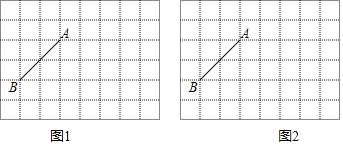
(1)在图1中画一个以线段AB为一边的矩形,点C、D均在小正方形的顶点上,且矩形ABCD的面积为4;
(2)在图2中画一个三角形△ABE,点E在小正方形的顶点上,且△ABE的面积为2,且∠AEB的正切值为![]() ,请直接写出BE的长.
,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
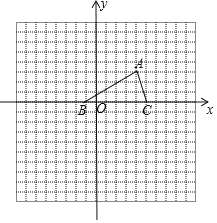
【题目】如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(﹣1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,则点C的对应点C1的坐标为 ;(不用画图)
(2)在图中画出将△ABC绕点B逆时针旋转90°得到的△A′BC′;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使S△ABC:S![]() =1:4,在图中画出△AB2C2.
=1:4,在图中画出△AB2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com