
【题目】如图,正方形ABCD的边长是3,延长AB至点P、延长BC至点Q,使BP=CQ,连接AQ,DP交于点O,相Q交CD于点F,DP交BC于点E,连接AE.
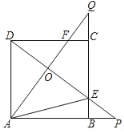
(1)求证:AQ⊥DP;
(2)求证:S△AOD=S四边形OECF;
(3)当BP=1时,请直接写出OE:OA的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由四边形ABCD是正方形,得到AD=BC,∠DAB=∠ABC=90°,根据全等三角形的性质得到∠P=∠Q,根据余角的性质得到AQ⊥DP;
(2)证明△CQF≌△BPE,根据全等三角形的性质得到CF=BE,DF=CE,于是得到S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF;
(3)证明△PBE∽△PAD,根据相似三角形的性质得到BE=![]() ,求出QE=
,求出QE=![]() ,OQ=
,OQ=![]() ,OE=
,OE=![]() ,即可求出OE:OA的值.
,即可求出OE:OA的值.
(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
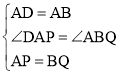 ,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
(2)证明:在△CQF与△BPE中,
 ,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
 ,
,
∴△ADF≌△DCE(SAS),
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
∴S△AOD=S四边形OECF;
(3)解:∵BP=1,AB=3,
∴PA=4,
∵△PBE∽△PAD,
∴![]() ,
,
∴![]() ,
,
∴QE=CQ+BC﹣CE=1+3﹣![]() ,
,
∵AD∥QE,
∴△QOE∽△PAD,
∴ ,
,
∴OQ=![]() ,OE=
,OE=![]() ,
,
∴![]() ,
,
∴ .
.


科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的函数关系图象,其中M为曲线部分的最低点下列说法错误的是( )
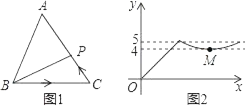
A. △ABC是等腰三角形B. AC边上的高为4
C. △ABC的周长为16D. △ABC的面积为10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,b)是双曲线y=![]() (x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(1)△PAC的面积是 ;
(2)当a=2,P点的坐标为(﹣2,0)时,求△ACB的面积;
(3)当a=2,P点的坐标为(x,0)时,设△ACB的面积为S,试求S与x之间的函数关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】豆豆妈妈用小米运动手环记录每天的运动情况,下面是她6天的数据记录(不完整):
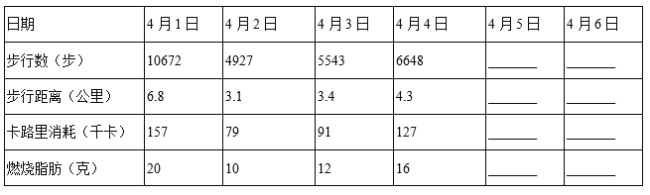
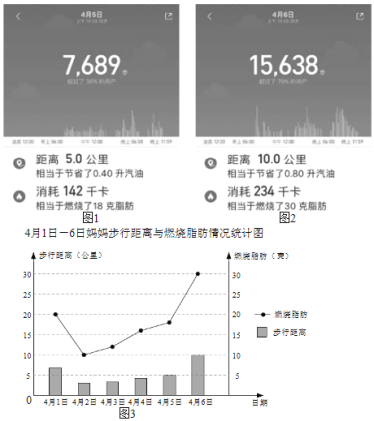
(1)4月5日,4月6日,豆豆妈妈没来得及作记录,只有手机图片,请你根据图片数据,帮她补全表格.
(2)豆豆利用自己学习的统计知识,把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来,请你根据图中提供的信息写出结论: .(写一条即可)
(3)豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系,豆豆妈妈想使自己的卡路里消耗数达到250千卡,预估她一天步行距离为 公里.(直接写出结果,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
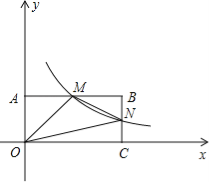
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三上学期期末考试后,数学老师将九年级(1)班的数学成绩制成如图所示的统计图(满分150分,每组含最低分,不含最高分),并给出如下信息:①第二组频率是0.15;②第二、四组的频率和是0.4;③自左至右第三,四,五,六,七组的频数比9:10:7:3:3.请你结合统计图解答下列问题:
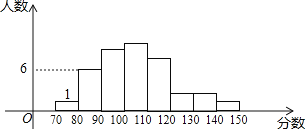
(1)九年级(1)班学生共有____人;
(2)求九年级(1)班在110~120分数段的人数;
(3)如果成绩不少于120分为优秀,那么全年级800人中成绩达到优秀的大约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.

① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+ ![]() (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).
(2)【解决问题】
直接写出“问题情境”中问题的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
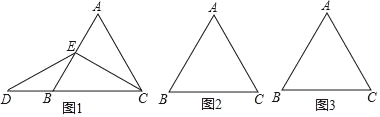
【题目】在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.
(1)如图1,AB=1,点E是AB的中点,求BD的长;
(2)点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;
(3)点E不在线段AB上,请在图3中画出符合条件的一个图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点D是边AB上的动点,将△ACD沿CD所在的直线折叠至△CDA的位置,CA'交AB于点E.若△A'ED为直角三角形,则AD的长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com