
【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.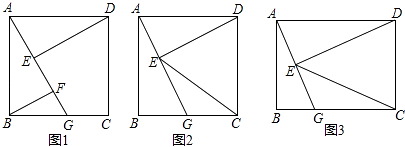
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG= ![]() BG,求
BG,求 ![]() ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)
【答案】
(1)证明:∵四边形ABCD为矩形,AB=BC,
∴四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,
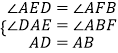
∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF﹣BF=EF,
(2)解:如图2,延长AG与DC交于点F,
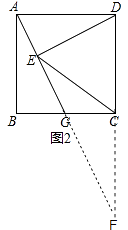
∵AG= ![]() BG,设BG=t,则AG=
BG,设BG=t,则AG= ![]() t,
t,
在Rt△ABG中,AB= ![]() =2t,
=2t,
∴G为BC的中点,
在△ABG和△FCG中,
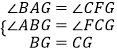
∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴ ![]() =
= ![]() =
= ![]()
(3)![]()
【解析】解:(3)如图3,连接DG,作EM⊥BC于M点,

∵DE⊥AG,DE=2,GE=1,
∴在Rt△DEG中,DG= ![]() =
= ![]() =
= ![]() ,
,
∵CG=CD,
∴在Rt△DCG中,∠CDG=∠CGD=45°,
∴CD=CG= ![]() =
= ![]() ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴ ![]() =
= ![]() ,
,
设AD=x,则AE= ![]() =
= ![]() ,AG=
,AG= ![]() +1,
+1,
∴ ![]() =
= ![]() ,
,
解得x1= ![]() ,x2=﹣2
,x2=﹣2 ![]() (舍去)
(舍去)
∴AE= ![]() =
= ![]() ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]()
解得EM= ![]() ,MG=
,MG= ![]() ,
,
∴CM=CG+MG= ![]() +
+ ![]() =
= ![]() ,
,
∴CE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
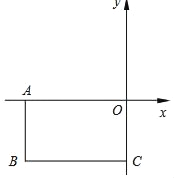
【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.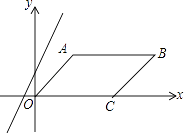
查看答案和解析>>
科目:初中数学 来源: 题型:
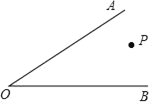
【题目】∠AOB内部有一点P,∠AOB=60°.
(1)过点P画PC∥OB,交OA于点C;
(2)过点P画PD⊥OB,交OB于点D,交OA于点E;
(3)过点C画直线OB的垂线段CF;
(4)根据所画图形,∠ACF= 度,∠OED= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,第一次将![]() 变换成
变换成![]() ,第二次将
,第二次将![]() 变换成
变换成![]() ,第三次将
,第三次将![]() 变换成
变换成![]() ,已知:
,已知:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
![]() 、
、![]() .若将
.若将![]() 进行了
进行了![]() (
(![]() ,且
,且![]() 为整数)次变换,得到
为整数)次变换,得到![]() ,推测
,推测![]() 的坐标是_____,
的坐标是_____,![]() 点的坐标是_______.
点的坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.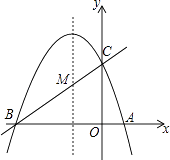
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() .
.
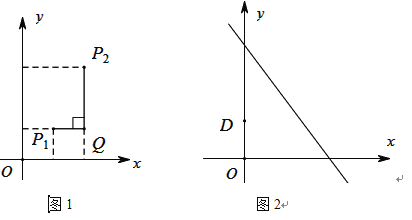
例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点
长度的较大值(点![]() 为垂直于
为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点![]() ,
,![]() 为
为![]() 轴上的一个动点.
轴上的一个动点.
①若点![]() (0,3),则点
(0,3),则点![]() 与点
与点![]() 的“非常距离”为 ;
的“非常距离”为 ;
②若点![]() 与点
与点![]() 的“非常距离”为2,则点
的“非常距离”为2,则点![]() 的坐标为 ;
的坐标为 ;
③直接写出点![]() 与点
与点![]() 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;
(2)已知点![]() (0,1),点
(0,1),点![]() 是直线
是直线![]() 上的一个动点,如图2,求点
上的一个动点,如图2,求点![]() 与点
与点![]() “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,请分别在图1、图2中各画一条线段,各图均满足以下要求: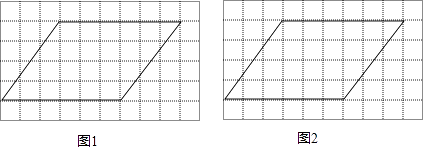
线段的一个端点为平行四边形的顶点,另一个端点在平行四边形一边的格点上(每个小正方形的顶点均为格点);
将平行四边形分割成两个图形,图1、图2中的分法各不相同,但都要求其中一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com