Question

【题目】（满分8分）如图，正方形ABCD中对角线AC、BD相交于O，E为AC上一点，AG⊥EB交EB于G，AG交BD于F.

(1)说明OE=OF的道理；

(2)在（1）中，若E为AC延长线上，AG⊥EB交EB的延长线于G，AG、BD的延长线交于F，其他条件不变，如图2，则结论：“OE=OF”还成立吗？请说明理由.

Answer 1

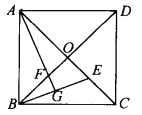
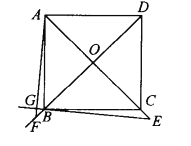
【答案】(1)见解析；（2）见解析.

【解析】试题分析：（1）根据正方形的性质利用ASA判定△AOF≌△BOE，根据全等三角形的对应边相等得到OE=OF；（2）类比（1）的方法证得同理得出结论成立．

试题解析：（1），在正方形ABCD中，

∴AO=BO,∠AOF=∠BOE=90°，

∴∠OBE+∠BEO=90°，

∵AG⊥EB，

∴∠AGE=90°，

∴∠GAE+∠AEG=90°，

∴∠OBE=∠OAF，

在△AOF和△BOE中，

，

∴△AOF≌△BOE(ASA)，

∴OE=OF.

(2)OE=OF仍然成立。

理由：正方形ABCD中,∴AO=BO,∠AOF=∠BOE=90°，

∴∠FAO+∠F=90°，

∵AG⊥EB,∴∠AGE=90°，

∴∠GAE+∠E=90°，

∴∠E=∠F，

在△AOF和△BOE中，

，

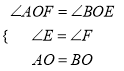∴△AOF≌△BOE(AAS)，

∴OE=OF.

所以结论仍然成立。