
分析 先设出满足条件的三位数,由于此三位数是11的倍数,故a-b+c=0或a-b+c=11,①当a-b+c=0时,根据题意列出方程组即可求出a、b、c的值;②当a-b+c=11时,根据题意列出关于a、b、c的方程,再根据c为奇数求出符合条件的a、b、c的值即可.
解答 解:设满足条件的三位数为$\overline{abc}$,
①若$\left\{\begin{array}{l}{a-b+c=0(1)}\\{100a+10b+c=11({a}^{2}+{b}^{2}+{c}^{2})(2)}\end{array}\right.$,
消去b得a2+a(c-5)+(c2-$\frac{c}{3}$)=0(3),
于是c为偶数,把c=0,2,4,6,8代入(3)试验,仅当c=0时,a为正整数,故当a-b+c=0时,a=5,b=5,c=0.
②若a-b+c=11(4),
100a+10b+c=11(a2+b2+c2)(5),
由(4)(5)消去b得,2a2+2c2+2ac-32a-23c+131=0(6),
易知c为奇数,把c=1,5,7,9代入(6)进行试验,仅当c=3时,a为正整数,故当a-b+c=11时,$\left\{\begin{array}{l}{a=8}\\{b=0}\\{c=3}\end{array}\right.$,
故符合条件的三位数是550,803.
故答案为:550,803.
点评 本题考查的是数的整除性问题,根据题意列出关于a、b、c的方程组是解答此题的关键.注意分类思想的运用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
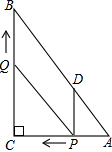 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c=asinA | B. | c=$\frac{a}{sinA}$ | C. | a=btanA | D. | c=$\frac{a}{cosA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平原上有四个村庄A、B、C、D,为解决当地缺水是问题,政府准备投资修建一个蓄水池到四个村庄的距离之和最小,如图,蓄水池应该建在点P处,运用的数学道理是两点之间线段最短.
平原上有四个村庄A、B、C、D,为解决当地缺水是问题,政府准备投资修建一个蓄水池到四个村庄的距离之和最小,如图,蓄水池应该建在点P处,运用的数学道理是两点之间线段最短.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com