
【题目】如图,一次函数y=x+1的图象与反比例函数y=![]() (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数y=x+1的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.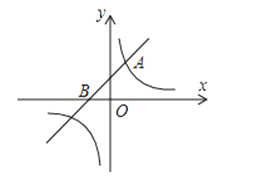
科目:初中数学 来源: 题型:
【题目】已知直线![]() 经过点
经过点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)把直线![]() 向右平移并与
向右平移并与![]() 轴相交于
轴相交于![]() 得到
得到![]() ,请在如图所示平面直角坐标系中作出直线
,请在如图所示平面直角坐标系中作出直线![]() ;
;
(3)若直线![]() 与
与![]() 轴交于
轴交于![]() 点,与直线
点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 解下列各题
(1)解方程x+![]() ;
;
(2)在解方程练习时,学习卷中有一个方程“2y﹣![]() =
=![]() y+■”中的■没印清,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时,代数式5(x﹣1)﹣2(x﹣2)﹣4的值相同,”小聪很快补上了这个常数,同学们,你们能补上这个常数吗?
y+■”中的■没印清,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时,代数式5(x﹣1)﹣2(x﹣2)﹣4的值相同,”小聪很快补上了这个常数,同学们,你们能补上这个常数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点E为正方形ABCD边BC上的一点,点G为BC延长线一点,连接AE,过点E作AE⊥EF,且AE=EF,连接CF.
(1)如图1,求证:∠FCG=45°,
(2)如图2,过点D作DH//EF交AB于点H,连接HE,求证:![]() ;
;
(3)如图3,连接AF、DF,若AF交CD于点M,DM=2,BH=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC的中心,射线OE交AB边于点E,OF交BC边于点F,若△ABC的面积为S,∠EOF=120°,则当∠EOF绕点O旋转时,得到的阴影面积发生变化吗?下面有三名同学提出了各自的观点.
甲:阴影部分的面积会发生变化,且当OE,OF分别与△ABC的边垂直时,阴影部分的面积最小.
乙:阴影部分的面积会发生变化,且当E,F分别与△ABC的顶点重合时,阴影部分的面积最大.
丙:无论怎样旋转,阴影部分的面积都保持不变.
你支持谁的观点?____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为 16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com