Question

【题目】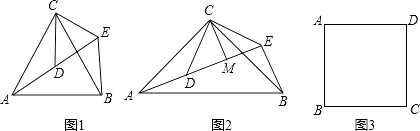
（1）问题发现 如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：
①∠AEB的度数为；
②线段AD，BE之间的数量关系为 ．
（2）拓展探究 如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．
（3）解决问题 如图3，在正方形ABCD中，CD= ，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．

Answer 1

【答案】
（1）60°；AD=BE
（2）解：∠AEB=90°，AE=BE+2CM．

理由：如图2，

∵△ACB和△DCE均为等腰直角三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=90°．

∴∠ACD=∠BCE．

在△ACD和△BCE中，

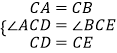
∴△ACD≌△BCE（SAS）．

∴AD=BE，∠ADC=∠BEC．

∵△DCE为等腰直角三角形，

∴∠CDE=∠CED=45°．

∵点A，D，E在同一直线上，

∴∠ADC=135°．

∴∠BEC=135°．

∴∠AEB=∠BEC﹣∠CED=90°．

∵CD=CE，CM⊥DE，

∴DM=ME．

∵∠DCE=90°，

∴DM=ME=CM．

∴AE=AD+DE=BE+2CM．

（3）解：点A到BP的距离为 或 ．

理由如下：

∵PD=1，

∴点P在以点D为圆心，1为半径的圆上．

∵∠BPD=90°，

∴点P在以BD为直径的圆上．

∴点P是这两圆的交点．

①当点P在如图3①所示位置时，

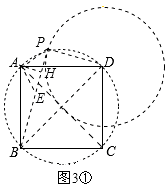
连接PD、PB、PA，作AH⊥BP，垂足为H，

过点A作AE⊥AP，交BP于点E，如图3①．

∵四边形ABCD是正方形，

∴∠ADB=45°．AB=AD=DC=BC= ，∠BAD=90°．

∴BD=2．

∵DP=1，

∴BP= ．

∵∠BPD=∠BAD=90°，

∴A、P、D、B在以BD为直径的圆上，

∴∠APB=∠ADB=45°．

∴△PAE是等腰直角三角形．

又∵△BAD是等腰直角三角形，点B、E、P共线，AH⊥BP，

∴由（2）中的结论可得：BP=2AH+PD．

∴ =2AH+1．

∴AH= ．

②当点P在如图3②所示位置时，

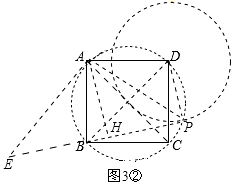
连接PD、PB、PA，作AH⊥BP，垂足为H，

过点A作AE⊥AP，交PB的延长线于点E，如图3②．

同理可得：BP=2AH﹣PD．

∴ =2AH﹣1．

∴AH= ．

综上所述：点A到BP的距离为 或 ．

【解析】解：（1）①如图1， ∵△ACB和△DCE均为等边三角形，
∴CA=CB，CD=CE，∠ACB=∠DCE=60°．
∴∠ACD=∠BCE．
在△ACD和△BCE中，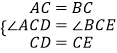

∴△ACD≌△BCE（SAS）．
∴∠ADC=∠BEC．
∵△DCE为等边三角形，
∴∠CDE=∠CED=60°．
∵点A，D，E在同一直线上，
∴∠ADC=120°．
∴∠BEC=120°．
∴∠AEB=∠BEC﹣∠CED=60°．
所以答案是：60°．
②∵△ACD≌△BCE，
∴AD=BE．
所以答案是：AD=BE．

【考点精析】本题主要考查了等腰三角形的性质和等边三角形的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．