
【题目】某水果公司以2.2元/千克的成本价购进![]() 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果损坏的频率 | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为______精确到0.1),据此,若公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为______元/千克.
【答案】0.1 5
【解析】
根据利用频率估计概率得到随实验次数的增多,发芽的频率越来越稳定在0.1左右,由此可估计苹果的损坏概率为0.1;根据概率计算出完好苹果的质量为10000×0.9=9000千克,设每千克苹果的销售价为x元,然后根据“售价=进价+利润”列方程解答.
解:根据表中的损坏的频率,当实验次数的增多时,苹果损坏的频率越来越稳定在0.1左右,
所以苹果的损坏概率为0.1.
根据估计的概率可以知道,在10000千克苹果中完好苹果的质量为10000×0.9=9000千克.
设每千克苹果的销售价为x元,则应有9000x=2.2×10000+23000,
解得x=5.
答:出售苹果时每千克大约定价为5元可获利润23000元.
故答案为:0.1,5.


科目:初中数学 来源: 题型:
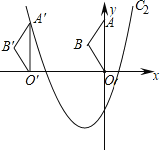
【题目】在平面直角坐标系中,将抛物线C1:y=x2﹣2x向左平移2个单位,向下平移3个单位得到新抛物线C2.
(1)求新抛物线C2的表达式;
(2)如图,将△OAB沿x轴向左平移得到△O′A′B′,点A(0,5)的对应点A′落在平移后的新抛物线C2上,求点B与其对应点B′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,0),B(0,4),现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1)求C点坐标及直线BC的解析式:
(2)点P从点A开始以每秒2个单位长度的速度匀速沿着x轴向右运动,若运动时间用t秒表示.△BCP的面积用S表示,请你直接写出S与t的函数关系.
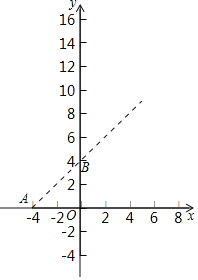
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.

根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为![]() 平方米,缴纳房款y万元,请求出
平方米,缴纳房款y万元,请求出![]() 关于x的函数关系式;
关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且 57<y≤60 时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
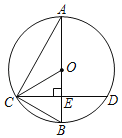
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户需求生产一种产品,成本每件20万元,规定每件售价不低于成本,且不高于40万元。经市场调查,每年的销售量y(件)与每件售价x(万元)满足一次函数关系,部分数据如下表:
售价x(万元/件) | 25 | 30 | 35 |
销售量y(件) | 50 | 40 | 30 |
(1)求y与x之间的函数表达式;
(2)设商品每年的总利润为W(万元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少万元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
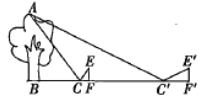
【题目】小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点![]() 处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得
处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得![]() m,
m,![]() m,
m,![]() m.求这棵古松树的高度.
m.求这棵古松树的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com