
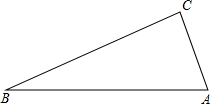
 如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决.
如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决. 分析 可以提出问题:(1)判断△ABC的形状;(2)求△ABC的面积.已知△ABC的三边,利用勾股定理的逆定理即可判断△ABC的形状;根据三角形的面积公式即可求出△ABC的面积.
解答 问题:(1)判断△ABC的形状;(2)求△ABC的面积.
解:(1)∵在△ABC中,AB=25,AC=7,BC=24,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且∠C=90°;
(2)∵在△ABC中,∠C=90°,
∴△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×7×24=84.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.在运用勾股定理的逆定理时,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.也考查了三角形的面积.注意,本题是开放性试题,答案不唯一.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
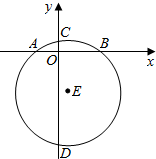 如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A、B,交y轴于点C、D,且点A、B的坐标分别为(-2,0)、(4,0).试求圆心E和点C、D的坐标.
如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A、B,交y轴于点C、D,且点A、B的坐标分别为(-2,0)、(4,0).试求圆心E和点C、D的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
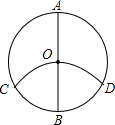 如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.
如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
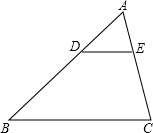 如图,已知△ABC∽△ADE,$\frac{AB}{BD}$=$\frac{5}{3}$,BC=20cm,∠BAC=40°,∠ABC=65°,求
如图,已知△ABC∽△ADE,$\frac{AB}{BD}$=$\frac{5}{3}$,BC=20cm,∠BAC=40°,∠ABC=65°,求查看答案和解析>>
科目:初中数学 来源: 题型:解答题
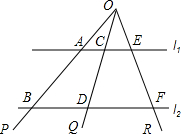 如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.
如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>m | B. | x>n | C. | x<m | D. | x<n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 北偏东36° | B. | 北偏西36° | C. | 北偏东54° | D. | 北偏西54° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com