
科目:初中数学 来源: 题型:
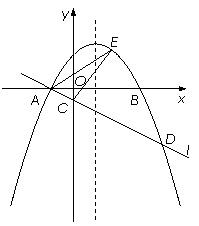
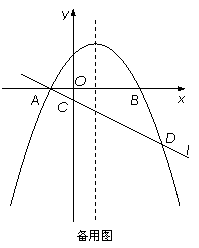
如图,在平面直角坐标系xOy中,抛物线y=ax 2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 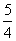 ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
 |  | ||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在3x3的正方形网格中有四个格点A, B, C, D,,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A.A点 B. B 点 C. C点 D. D
点 C. C点 D. D 点
点

查看答案和解析>>
科目:初中数学 来源: 题型:
定义:长宽比为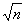 :1(n为正基数)的矩形称为株为
:1(n为正基数)的矩形称为株为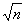 矩形. 下面,我们通过折叠的方式折出一个
矩形. 下面,我们通过折叠的方式折出一个 矩形.
矩形. 如图①所示.
如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF
则四 边形BCEF为
边形BCEF为 矩形
矩形
证明:设正方形ABCD的边长为1,则BD=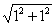 =
= .
.
由折叠性质可知BG=BC=1,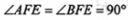 ,则四边形BCEF为矩形
,则四边形BCEF为矩形

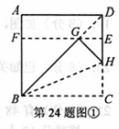
阅读以上内容,回答下列问题:
(1) 在图 中,所有与CH相等的线段是 ,tan
中,所有与CH相等的线段是 ,tan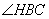 的值是
的值是
(2) 已知四边形BCEF为 矩形,模仿上述操作,得到四边形BCMN,如图
矩形,模仿上述操作,得到四边形BCMN,如图 。
。
求证:四边形BCMN是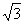 矩形
矩形
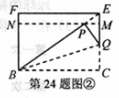
将图 中的
中的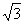 矩形BCM
矩形BCM N沿用(2)中的操作3次后,得到一个“
N沿用(2)中的操作3次后,得到一个“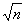 矩形”,则n的值是
矩形”,则n的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式 (
(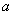 是多边形内的格点数,
是多边形内的格点数, 是多边形边界上的格点数)计算,这个公式称为“皮克定理”。现有一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.
是多边形边界上的格点数)计算,这个公式称为“皮克定理”。现有一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.
(1)这个格点多边形边界上的格点数 = (用含
= (用含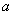 的代数式表示);
的代数式表示);
(2)设该格点多边形外的格点数为 ,则
,则 =
=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com