
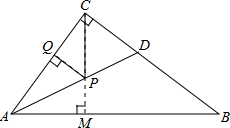
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,求PC+PQ的最小值.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,求PC+PQ的最小值.| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 62+82 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
| 6×8 |
| 10 |
| 24 |
| 5 |
| 24 |
| 5 |


科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 7 |
| 12 |
| 5 |
| 9 |
| 1 |
| 36 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:PA、PC分别是△ABC外角∠MAC与∠NCA的平分线,并交于点P,PD⊥BM于点D,PF⊥BN于点F.
如图:PA、PC分别是△ABC外角∠MAC与∠NCA的平分线,并交于点P,PD⊥BM于点D,PF⊥BN于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号;小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小华步行速度为24米/分,小明步行速度为32米/分,恰好在出发后10分钟后信号开始不清楚.求出他们研制的信号收发系统的信号传送半径?(以信号清晰为界限,请在图中画出示意图后再解答)
学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号;小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小华步行速度为24米/分,小明步行速度为32米/分,恰好在出发后10分钟后信号开始不清楚.求出他们研制的信号收发系统的信号传送半径?(以信号清晰为界限,请在图中画出示意图后再解答)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com