
����Ŀ����ͼ����֪һ��ֱ�߹��㣨0��4��������������y= ![]() x2����A��B���㣬���е�A�ĺ������ǩ�2��
x2����A��B���㣬���е�A�ĺ������ǩ�2��
��1��������ֱ�ߵĺ�����ϵʽ����B�����꣮
��2����x�����Ƿ���ڵ�C��ʹ�á�ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
��3�����߶�AB��һ��P����PM��x�ᣬ���������ڵ�M����M�ڵ�һ���ޣ���N��0��1��������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�
���𰸡�
��1���⣺�ߵ�A��ֱ���������ߵĽ��㣬�Һ�����Ϊ��2��
��y= ![]() ������2��2=1��A�����������2��1����
������2��2=1��A�����������2��1����
��ֱ�ߵĺ�����ϵʽΪy=kx+b��
����0��4��������2��1������� ![]() ��
��
��� ![]() ��
��
��ֱ��y= ![]() x+4��
x+4��
��ֱ�����������ཻ��
�� ![]() x+4=
x+4= ![]() x2��
x2��
��ã�x=��2��x=8��
��x=8ʱ��y=16��
���B��������8��16��
��2����ͼ1������AC��BC�� 
����A����2��1����B��8��16�������AB2=325��
���C��m��0����ͬ���ɵ�AC2=��m+2��2+12=m2+4m+5��
BC2=��m��8��2+162=m2��16m+320��
������BAC=90�㣬��AB2+AC2=BC2����325+m2+4m+5=m2��16m+320��
��ã�m=�� ![]() ��
��
������ACB=90�㣬��AB2=AC2+BC2����325=m2+4m+5+m2��16m+320��
��ã�m=0��m=6��
������ABC=90�㣬��AB2+BC2=AC2����m2+4m+5=m2��16m+320+325��
��ã�m=32��
���C���������� ![]() ��0������0��0������6��0������32��0��
��0������0��0������6��0������32��0��
��3���⣺��M��a�� ![]() a2������ͼ2����MP��y�ύ�ڵ�Q��
a2������ͼ2����MP��y�ύ�ڵ�Q�� 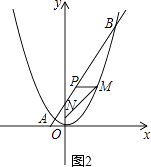
��Rt��MQN�У��ɹ��ɶ�����MN= ![]() =
= ![]() a2+1��
a2+1��
�֡ߵ�P���M��������ͬ��
�� ![]() +4=
+4= ![]() a2��
a2��
��x= ![]() ��
��
���P�ĺ�����Ϊ ![]() ��
��
��MP=a�� ![]() ��
��
��MN+3PM= ![]() +1+3��a��
+1+3��a�� ![]() ��=��
��=�� ![]() a2+3a+9��
a2+3a+9��
�൱a=�� ![]() =6��
=6��
�֡�2��6��8��
��ȡ�����ֵ18��
�൱M�ĺ�����Ϊ6ʱ��MN+3PM�ij��ȵ����ֵ��18��
����������1���������ߵĽ���ʽ����õ�A�������꣬Ȼ�����ô���ϵ����ȷ��ֱ�ߵĽ���ʽ����ֱ�ߺ������ߵĽ���ʽ��������ý�������ꣻ
��2������B��BG��x�ᣬ����A��AG��y�ᣬ����ΪG��Ȼ�������BAC=90�㣬��AB2+AC2=BC2������ACB=90�㣬��AB2=AC2+BC2������ABC=90�㣬��AB2+BC2=AC2����������m��ֵ���Ӷ�ȷ����C�����ꣻ
��3����M��a��![]() a2����MP��y�ύ�ڵ�Q����Rt��MQN�����ݹ��ɶ��������MN�ij����ú�a��ʽ�ӱ�ʾ����Ȼ����ݵ�P���M��������ͬ�õ�x=
a2����MP��y�ύ�ڵ�Q����Rt��MQN�����ݹ��ɶ��������MN�ij����ú�a��ʽ�ӱ�ʾ����Ȼ����ݵ�P���M��������ͬ�õ�x=![]() ���Ӷ��õ�MN+3PM����a�ĺ�����ϵ�ǣ�������ݶ��κ��������ʿɵõ�MN+3PM�ij��ȵ����ֵ.
���Ӷ��õ�MN+3PM����a�ĺ�����ϵ�ǣ�������ݶ��κ��������ʿɵõ�MN+3PM�ij��ȵ����ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ��ؽ���A��˳����ʻ��B�ۣ��ȴ�B�۷���A������3Сʱ��������Ϊ26ǧ��/ʱ��ˮ��Ϊ2ǧ��/ʱ����A�ۺ�B��������ǧ�ף���A�ۺ�B�����xǧ�ף��������⣬���г��ķ����ǣ�( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������P��2x��6��x��4����ƽ��ֱ������ϵ�ĵ��������ڣ���ôx��ȡֵ��Χ�������Ͽɱ�ʾΪ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�����������a��b��c����M{a��b��c}��ʾ����������ƽ��������min{a��b��c}��ʾ������������С���������磺M{��1��2��3}��![]() ��
��![]() ��min{��1��2��3}����1��min{��1��2��a}��
��min{��1��2��3}����1��min{��1��2��a}��![]()
����������⣺
��1����min{2��2x+2��4��2x}��2����x�ķ�Χ__________��
��2�������M{2��x+1��2x}��min{2��x+1��2x}����x��
�����������㷢���˽��������M{a��b��c}��min{a��b��c}����ô__________����a��b��c�Ĵ�С��ϵ������
���������Ľ��ۣ���M{2x+y+2��x+2y��2x��y}��min{2x+y+2��x+2y��2x��y}����x+y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB����һ�����C����M���߶�AC���е㣬��N���߶�BC���е㣬��AB=6cmʱ��
��1�����߶�MN�ij���
��2����C��AB�ӳ�����ʱ�������������䣬���߶�MN�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=kx+b�ͷ���������y2= ![]() ��ͼ����A��B���㣮
��ͼ����A��B���㣮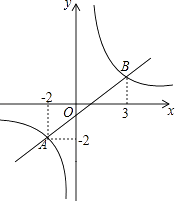
��1����һ�κ���y1=kx+b�ͷ���������y2= ![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���۲�ͼ��д��y1��y2ʱ��x��ȡֵ��ΧΪ��
��3�����OAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
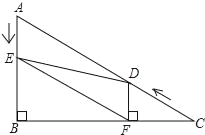
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��10����C��30����D�ӵ�C������CA������ÿ��2����λ���ȵ��ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ���ȵ��ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
��1��DF���� �������ú�t�Ĵ���ʽ��ʾ��
��2����֤����AED�ա�FDE��
��3����tΪ��ֵʱ����DEF�ǵȱ������Σ�˵�����ɣ�
��4����tΪ��ֵʱ����DEFΪֱ�������Σ�����ֱ��д��t��ֵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��С����һ����
��С����һ����![]() ��ֱ�����ǰ�
��ֱ�����ǰ�![]() ��ͼ1��ʾ���ã�ʹ����
��ͼ1��ʾ���ã�ʹ����![]() ����ֱ��
����ֱ��![]() �ϣ�����
�ϣ�����![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() (��
(��![]() ��
��![]() ���)��
���)��

��1����![]() ��
��![]() ����
����![]() __________
__________![]() ��
��
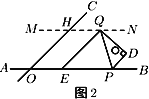
��2����![]() �Ľ�ƽ���߽�ֱ��
�Ľ�ƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ͼ2��
����ͼ2��

����![]() ��
��![]() ʱ����֤��
ʱ����֤��![]() ��
��
��С�������ǰ屣��![]() ������ƽ�ƣ��˶������У�
������ƽ�ƣ��˶������У�![]() __________��(��
__________��(��![]() ��ʾ)��
��ʾ)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com