
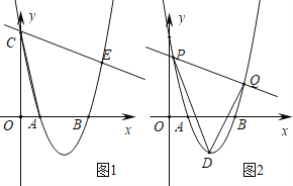
【题目】如图,已知抛物线![]() 与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
(1)求抛物线的解析式;
(2)如图1,过点C的直线交抛物线于另一点E,若∠ACE=60°,求点E的坐标.
(3)如图2,直线![]() 交抛物线于P,Q两点,求△DPQ面积的最小值.
交抛物线于P,Q两点,求△DPQ面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)△DPQ面积的最小值为
;(3)△DPQ面积的最小值为![]()
【解析】
(1)由抛物线与x轴的两个交点坐标A(1,0),B(3,0),可代入点的坐标即可得解;
(2)过点A作AF⊥AC交AC的延长线于点F,过点F作FG⊥x轴交x轴于点G,可证明△AOC∽△FGA,利用60°角的锐角三角函数值和比例线段可求出AG和FG的长,则F点坐标为(10,![]() ),求得直线CF的解析式,与抛物线方程联立即求出点E的坐标;
),求得直线CF的解析式,与抛物线方程联立即求出点E的坐标;
(3)过点D作DM∥y轴交PQ于点M,由抛物线顶点D的坐标可知DM=2![]() ,若△DPQ面积有最小值,则底边是定值,点P和点Q的横坐标之差的绝对值最小.联立直线与抛物线方程可用k表示出点P和点Q的横坐标之差的绝对值,即可得解.
,若△DPQ面积有最小值,则底边是定值,点P和点Q的横坐标之差的绝对值最小.联立直线与抛物线方程可用k表示出点P和点Q的横坐标之差的绝对值,即可得解.
解:(1)∵抛物线y=ax2+bx+3![]() 与x轴交于A(1,0),B(3,0)两点
与x轴交于A(1,0),B(3,0)两点
∴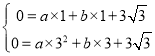
解得:a=![]() ,b=
,b=![]() ;
;
∴所求抛物线的解析式为:![]() ;
;
(2)如图1所示,过点A作AF⊥AC交CE的延长线于点F,过点F作FG⊥x轴交x轴于点G,
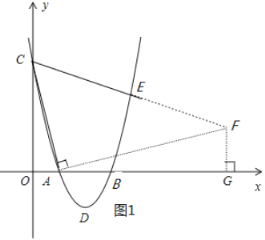
∵∠COA=∠CAF=∠FGA=90°,
∴∠OCA=∠GAF,∠OAC=∠GFA
∴△AOC∽△FGA,
∴![]()
又∵△CAF是直角三角形,∠ACE=60°
∴![]() ,
,
∴![]() ,
,
∵OC=3![]() ,OA=1,
,OA=1,
∴FG=![]() ,AG=9,
,AG=9,
∴F![]() ,
,
设直线CF的解析式为:y=mx+n,
将![]() 分别代入上式,
分别代入上式,
得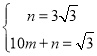 ,
,
解得: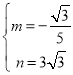 ,
,
∴直线CF的解析式为:![]() ,
,
联立直线CF与抛物线的解析式得
∴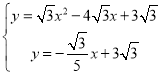 ,
,
解得: (不符合题意),
(不符合题意),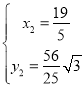 ,
,
∴所求点E的坐标为:![]() ;
;
(3)如图2,过点D作DM∥y轴交PQ于点M,
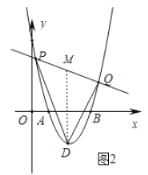
∵![]() =
=![]()
∴![]() ,
,
把x=2代入直线y=kx-2k+![]() 得y=
得y=![]() ,
,
∴DM=![]() ,
,
∵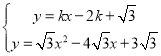 ,
,
整理得![]() ,
,
∴P、Q两点的横坐标x1、x2为方程![]() 的两根,
的两根,
∴![]() =
=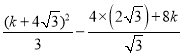 =
=![]() ,
,
当k=0时,![]() 的最小值为8,此时|x1-x2|的最小值为2
的最小值为8,此时|x1-x2|的最小值为2![]() .
.
∵![]() =
=![]() |x1-x2|.
|x1-x2|.
∴△DPQ面积的最小值为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
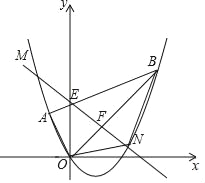
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,3,现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M的所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
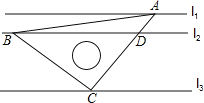
【题目】如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AB=AC,点F在边BC上

(1)如图1,AF=BF,求证:AB2=BFBC;
(2)如图2,FC=2BF,点E、M在直线AB上,EF∥AC,cosB=n,且FM2=MEMB
①若M在边AB上,求![]() 的值(用含n的式子表示);
的值(用含n的式子表示);
②若M在BA的延长线上时,直接写出n的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
(1) 求证:DE⊥AC;
(2) 连结OC交DE于点F,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com