
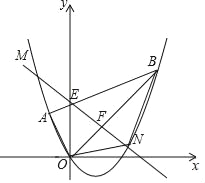
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
【答案】(1)E点坐标为(0,![]() );(2)
);(2)![]() ;(3)四边形ABNO面积的最大值为
;(3)四边形ABNO面积的最大值为![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,
,![]() ).
).
【解析】
(1)先利用待定系数法求直线AB的解析式,与y轴的交点即为点E;
(2)利用待定系数法抛物线的函数解析式;
(3)先设N(m,![]() m2
m2![]() m)(0<m<3),则G(m,m),根据面积和表示四边形ABNO的面积,利用二次函数的最大值可得结论.
m)(0<m<3),则G(m,m),根据面积和表示四边形ABNO的面积,利用二次函数的最大值可得结论.
(1)设直线AB的解析式为y=mx+n,
把A(-1,1),B(3,3)代入得![]() ,解得
,解得![]() ,
,
所以直线AB的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() ×0+
×0+![]() =
=![]() ,
,
所以E点坐标为(0,![]() );
);
(2)设抛物线解析式为y=ax2+bx+c,
把A(-1,1),B(3,3),O(0,0)代入得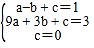 ,解得
,解得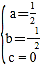 ,
,
所以抛物线解析式为y=![]() x2
x2![]() x;
x;
(3)如图,作NG∥y轴交OB于G,OB的解析式为y=x,
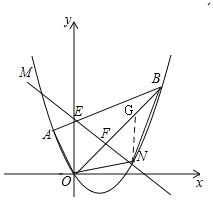
设N(m,![]() m2
m2![]() m)(0<m<3),则G(m,m),
m)(0<m<3),则G(m,m),
GN=m(![]() m2
m2![]() m)=
m)=![]() m2+
m2+![]() m,
m,
S△AOB=S△AOE+S△BOE=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=3,
×3=3,
S△BON=S△ONG+SBNG=![]() 3(
3(![]() m2+
m2+![]() m)=
m)=![]() m2+
m2+![]() m
m
所以S四边形ABNO=S△BON+S△AOB=![]() m2+
m2+![]() m+3=
m+3=![]() (m
(m![]() )2+
)2+![]()
当m=![]() 时,四边形ABNO面积的最大值,最大值为
时,四边形ABNO面积的最大值,最大值为![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.

(1)如图1,求证:![]() ;
;
(2)如图2,![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,当
,当![]() 的面积为
的面积为![]() 时, 求
时, 求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来我市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民租用“共享单车”的骑车时间![]() (单位:分),将获得的数据分成四组,绘制了如下统计图(
(单位:分),将获得的数据分成四组,绘制了如下统计图(![]() ),根据图中信息,解答下列问题:
),根据图中信息,解答下列问题:
(1)这项被调查的总人数是 人,表示![]() 组的扇形统计图的圆心角的度数为 .
组的扇形统计图的圆心角的度数为 .
(2)若某小区共有![]() 人,根据调查结果,估计租用“共享单车”的骑车时间为
人,根据调查结果,估计租用“共享单车”的骑车时间为![]() 的大约有多少人?
的大约有多少人?
(3)如果琪琪同学想从![]() 组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
①依题意补全图1;
②求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
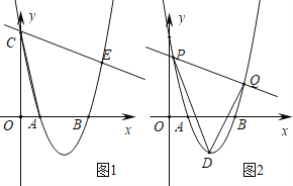
【题目】如图,已知抛物线![]() 与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
(1)求抛物线的解析式;
(2)如图1,过点C的直线交抛物线于另一点E,若∠ACE=60°,求点E的坐标.
(3)如图2,直线![]() 交抛物线于P,Q两点,求△DPQ面积的最小值.
交抛物线于P,Q两点,求△DPQ面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com