
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
①依题意补全图1;
②求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.

【答案】(1)①补全的图形如图1所示,见解析;②![]() ;(2)
;(2)![]()
【解析】
(1)利用平移的性质画出图形,再利用相似得出比例,即可求出线段DP的长.
(2)根据条件MQ=DP,利用平行四边形的性质和相似三角形的性质,求出BN的长即可解决.
(1)①如图1,补全图形

②连接AD,如图1.
在Rt△ABN中,
∵∠B=90°,AB=4,BN=1,
∴AN=![]()
∵线段AN平移得到线段DM,
∴DM=AN=![]() ,
,
AD=NM=1,AD∥MC,
∴△ADP∽△CMP.
∴![]()
∴DP=![]() ;
;
(2)连接NQ,

由平移知:AN∥DM,且AN=DM.
∵MQ=DP,
∴PQ=DM.
∴AN∥PQ,且AN=PQ.
∴四边形ANQP是平行四边形.
∴NQ∥AP.
∴∠BQN=∠BAC=45°.
又∵∠NBQ=∠ABC=90°,
∴BN=BQ.
∵AN∥MQ,
∴![]() .
.
又∵M是BC的中点,且AB=BC=4,
∴![]() .
.
∴NB=2![]() (负数舍去).
(负数舍去).
∴ME=BN=2![]() .
.
∴CE=2![]() 2
2


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
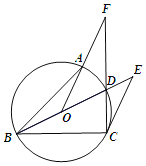
【题目】已知,如图,BD为⊙O的直径,点A、C在⊙O上并位于BD的两侧,∠ABC=45°,连结CD、OA并延长交于点F,过点C作⊙O的切线交BD延长线于点E.
(1)求证:∠F=∠ECF;
(2)当DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
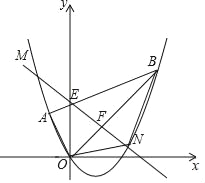
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
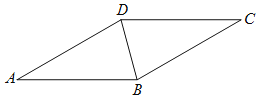
【题目】如图,BD是菱形ABCD的对角线.
(1)请用直尺和圆规作AB的垂直平分线EF,垂足为点E,交AD于点F;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,若∠CBD=75°,求∠DBF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著在数学上有其独到的成就,不仅最早提到了分数问题,首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱又会缺16文钱,问买鸡的人数、鸡的价格各是多少?通过计算可得买鸡的人数是( )
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
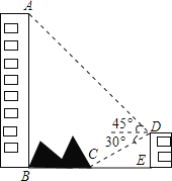
【题目】 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AB=AC,点F在边BC上

(1)如图1,AF=BF,求证:AB2=BFBC;
(2)如图2,FC=2BF,点E、M在直线AB上,EF∥AC,cosB=n,且FM2=MEMB
①若M在边AB上,求![]() 的值(用含n的式子表示);
的值(用含n的式子表示);
②若M在BA的延长线上时,直接写出n的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com