练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若∠A=32°18′，∠B=32.18°，∠C=32.3°，则下列结论正确的是（　　）
    A．∠B=∠CB．∠A=∠CC．∠A=∠BD．∠A＜∠B

    分析 根据小单位化成大单位除以进率，可统一成以度为单位的角，根据有理数的大小比较，可得答案．

    解答 解：∠A=32.3°=∠C＞∠B，
    故选：B．

    点评 本题考查了度分秒的换算，利用小单位化成大单位除以进率统一成以度为单位的角是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
    （1）若从中任取一个球，求摸出球上的汉字刚好是“美”的概率；
    （2）甲从中任取一球，不放回，再从中任取一球，请用树状图或列表法，求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知关于x的一元二次方程2x2+4x+k-1=0有实数根，k为正整数．
    （1）求k的值；
    （2）根据（1）的结论，当此方程有两个非零的整数根时，将二次函数=2x2+4x+k-1的图象向下平移4个单位．
    ①求平移后的图象所对应的函数关系式；
    ②在给定的网格中，画出平移后的大致图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．（1）计算：（-$\frac{1}{2}$）×22-2$÷\frac{1}{3}×3+$|-3|；
    （2）计算：（$\frac{1}{2}-\frac{1}{3}$）÷（-$\frac{1}{6}$）-（-2）2×（-3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

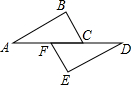    20．如图，在△ABC和△DEF中，已知∠BCA=∠EFD，∠B=∠E，要判定这两个三角形全等，还需要条件（　　）
    A．∠A=∠DB．AB=FDC．AC=EDD．AF=CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，已知点O到△ABC的两边AB、AC的距离分别是OD、OE，且OD=OE，OB=OC．
    （1）如图1，若点O在BC边上，补全图形并求证：AB=AC；
    （2）如图2，若点O在△ABC的内部，补全图形并求证：AB=AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知抛物线y=x2+（m+1）x+m-1与x轴交于A，B两点，顶点为C，则△ABC面积的最小值为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

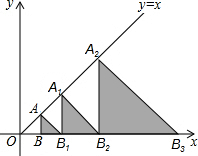    14．如图，点A，A1，A2，…都在直线y=x上，点B，B1，B2，B3，…都在x轴上，且△ABB1，△A1B1B2，△A2B2B3，…都是等腰直角三角形，若按如此规律排列下去，已知B（1，0），则A2016的坐标为（22016，22016）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-8，0），点B的坐标是（0，n）（n＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连接PP′，P′A，P′C．设点P的横坐标为m．
    （1）若点P在第一象限，记直线AB与P′C的交点为D．当P′D：DC=5：13时，求m的值；
    （2）若∠ACP′=60°，试用m的代数式表示n；
    （3）若点P在第一象限，是否同时存在m，n，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的m，n的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案