Question

15．如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-8，0），点B的坐标是（0，n）（n＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连接PP′，P′A，P′C．设点P的横坐标为m．
（1）若点P在第一象限，记直线AB与P′C的交点为D．当P′D：DC=5：13时，求m的值；
（2）若∠ACP′=60°，试用m的代数式表示n；
（3）若点P在第一象限，是否同时存在m，n，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的m，n的值；若不存在，请说明理由．

Answer 1

分析 （1）由条件可得△P′PD∽△CAD，利用相似三角形的性质可得到关于m的方程，可求得m的值；
（2）过P′H⊥AC于H，设直线AB的解析式为y=kx+n，把x=-8，y=0代入得：-8k+n=0，于是得到直线的解析式是：y=$\frac{n}{8}$x+n，求得PC=P′H=$\frac{mn}{8}$+n，根据三角函数的定义得到$\frac{P′H}{CH}$=$\sqrt{3}$，即可得到结论；
（3）分∠AP′C、∠P′AC和∠P′CA分别为直角进行讨论，由等腰三角形可先求得m的值，再根据相似三角形可得到关于n的方程，可求得n的值．

解答 解：（1）∵PP′∥AC，
∴△P′PD∽△CAD，
∴$\frac{P′P}{AC}$=$\frac{P′D}{DC}$=$\frac{5}{13}$，
∴$\frac{2m}{m+8}$=$\frac{5}{13}$，
解得：m=$\frac{40}{21}$；

（2）过P′H⊥AC于H，设直线AB的解析式为y=kx+n，
把x=-8，y=0代入得：-8k+n=0，
∴k=$\frac{n}{8}$，
∴直线的解析式是：y=$\frac{n}{8}$x+n，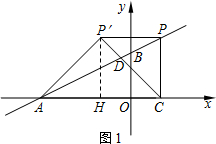
把x=m代入得y=$\frac{mn}{8}$+n，
∴PC=P′H=$\frac{mn}{8}$+n，
∵∠ACP′=60°，
∴$\frac{P′H}{CH}$=$\sqrt{3}$，
∴$\frac{\frac{mn}{8}+n}{2m}$=$\sqrt{3}$，
∴n=$\frac{{16\sqrt{3}m}}{8+m}$；

（3）当点P在第一象限且△P′CA为等腰直角三角形时，分∠AP′C、∠P′AC和∠P′CA分别为直角进行讨论．
第一种情况：
若∠AP′C=90°，P′A=P′C，
过点P′作P′H⊥x轴于点H．
∴PP′=CH=AH=P′H=$\frac{1}{2}$AC．
∴2m=$\frac{1}{2}$（m+8），
∴m=$\frac{8}{3}$，P′H=$\frac{16}{3}$，
∵△AOB∽△ACP，
∴$\frac{8}{n}=\frac{\frac{32}{3}}{\frac{16}{3}}$，
∴n=4；
第二种情况：
若∠P′AC=90°，P′A=AC，则PP′=AC，
∴2m=m+8，
∴m=8，
∵△P′AC为等腰直角三角形，
∴四边形P′ACP为正方形，
∴PC=AC=16，
∵△AOB∽△ACP，
∴$\frac{AO}{AC}=\frac{OB}{PC}$，即$\frac{8}{16}$=$\frac{n}{16}$，
∴n=8；
第三种情况：
若∠P′CA=90°，则点P′，P都在第一象限内，这与条件矛盾．
∴△P′CA不可能是以C为直角顶点的等腰直角三角形．
∴所有满足条件的m=$\frac{8}{3}$，n=4或m=8，n=8．

点评 本题主要考查相似三角形的判定和性质及等腰直角三角形的性质、坐标与图形等知识点的综合应用，在（1）中由条件证明三角形相似，利用相似三角形对应边成比例得到关于m的方程是解题的关键；在（3）中分三种情况分别讨论是解题的关键；属于基础知识的综合考查，难度不大，注意对基础知识的熟练应用．