
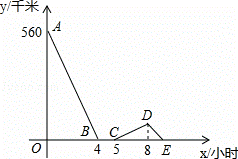
一辆慢车与一辆快车分别从甲、乙两地同 时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

解:(1)由题意可得出:甲乙两地之间的距离为560千米;
故答案为:560;
(2)由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大知直到 快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20
∴快车的速度是80km/h,慢车的速度是60km/h.
(3)由题意可得出:快车和慢车相遇地离甲地的距离为4×60=240km,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240﹣3×60=60km,
∴D(8,60),
∵慢车往返各需4小时,
∴E(9,0),
设DE的解析式为:y=kx+b,
∴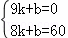 ,
,
解得: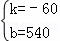 .
.
∴线段DE所表示的y与x之间的函数关系式为:y=﹣60x+540(8≤x≤9).


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
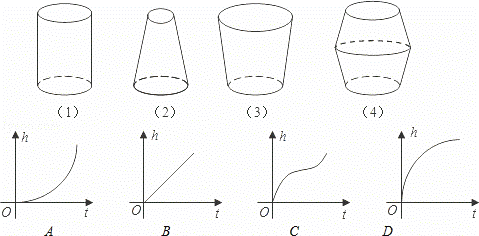
如图,水以恒速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,
(1)请分别找出与各容器对应的水的高度h和时间t的函数关系图象,用直线段连接起来;
(2)当容器中的水恰好达到一半高度时,请在函数关系图的t轴上标出此时t值对应点T的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若 某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
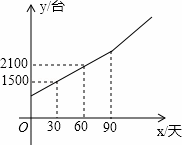
随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
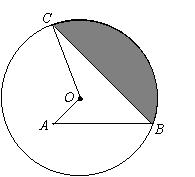
如图,已知点A为 内一点,点B、C均在圆上,∠C=30°,
内一点,点B、C均在圆上,∠C=30°,
|
|

 ∠A=∠B ,线段OA=
∠A=∠B ,线段OA=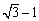 ,则阴影部分的周长为( )
,则阴影部分的周长为( )
|
|

 A.
A.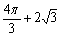 B.
B.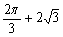
C.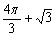 D.
D.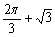
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某玩具经销商用3.2万元购进了一批玩具,上市后一个星期恰好全部售完,该经销商又用6.8万元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该经销商两次共购进这种玩具多少套?
(2)若第一批玩具售完后的总利润率为25%,购进第二批玩具后由于进价上涨,准备调整价
格,发现若每套涨价1元,则每星期会少卖5套,问该经销商第二批玩具应该如何定价才能使利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com