
【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

【答案】(1)∠BCE=90°;(2)![]() .
.
【解析】试题分析:
(1)由已知条件证△ABD≌△ACE,可得∠ACE=∠B=45°,从而可得∠BCE=∠ACE+∠ACB=90°;
(2)同(1)由已知条件证△ABD≌△ACE,可得CE=BD=5及∠ACE=∠ABD=180°-45°=135°,从而可得∠DCE=∠ACE-∠ACB=90°,这样在Rt△DCE中由勾股定理可求得DE的长,再过点A作AF⊥DE于点F,由等腰三角形和直角三角形的性质可得AF=![]() DE,这样就可由S△ADE=
DE,这样就可由S△ADE=![]() DE
DE![]() AF求得面积了.
AF求得面积了.
试题解析:
(1)如图1,∵ ∠BAC=90°,∠DAE=90°,
∴ ∠BAD+∠DAC=90°,∠EAC+∠DAC=90°,
∴ ∠BAD=∠EAC .
在△ABD和△ACE中, 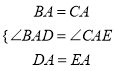 ,
,
∴ △ABD≌△ACE (SAS)
∴ ∠ACE=∠B
∵ ∠BAC=90°
∴ ∠B+∠ACB=90°
∴ ∠ACE+∠ACB=90° 即:∠BCE=90°.
(2) 如图2,过点A作AF⊥DE于点F.
∵ AD=AE,
∴ 点F是DE的中点.
∵ ∠DAE=90°,
∴![]() .
.
同(1)可证:△ABD≌△ACE,
∴EC=BD=5,∠ABD=∠ACE=180°-∠ABC=135°,
∴∠DCE=∠ACE-∠ACB=90°,
又∵DC=BD+BC=5+7=12,
∴DE=![]() .
.
∴AF=![]() .
.
∴ △ADE的面积为=![]()



 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】下列所给的各组线段,能组成三角形的是( )
A. 10cm、20cm、30cm B. 20cm、30cm、40cm
C. 10cm、20cm、40cm D. 10cm、40cm、50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划用104 000元购置一批电脑(这批款项须恰好用完,不得剩余或追加).经过招标,其中平板电脑每台1600元,台式电脑每台4000元,笔记本电脑每台4600元.
(1)若学校同时购进其中两种不同类型的电脑共50台,请你帮学校设计该如何购买;
(2)若学校同时购进三种不同类型的电脑共26台(三种类型的电脑都有),并且要求笔记本电脑的购买量不少于15台,请你帮学校设计购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知矩形A的长、宽分别是2和1,那么是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决.小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4.请你按照小明的论证思路完成后面的论证过程.(画图并简单的文字说明)
(2)已知矩形A的长和宽分别是2和1,那么是否存在一个矩形C,它的周长和面积分别是矩形A的周长和面积的一半?小明认为这个问题是肯定的,你同意小明的观点吗?为什么?(同上要求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( ) 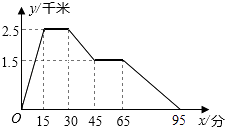
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
D.张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com