Question

【题目】已知：正方形ABCD，E是BC的中点，连接AE，过点B作射线BM交正方形的一边于点F，交AE于点O．

（1）若BF⊥AE，

①求证：BF＝AE；

②连接OD，确定OD与AB的数量关系，并证明；

（2）若正方形的边长为4，且BF＝AE，求BO的长．

Answer 1

【答案】（1）①见解析；②OD＝AB．证明见解析；（2）①BO＝或BO＝.

【解析】

（1）①如图1①，要证BF＝AE，只需证△ABE≌△BCF，只需证到∠BAE＝∠CBF即可；

②延长AD，交射线BM于点G，如图1②，由△ABE≌△BCF可得BE＝CF，由此可得CF＝DF，从而可证到△DGF≌△CBF，则有DG＝BC，从而可得DG＝AD，然后运用直角三角形斜边上的中线等于斜边的一半即可解决问题；

（2）可分点F在CD上和点F在AD上两种情况进行讨论．当点F在CD上时，如图2①，易证Rt△ABE≌Rt△BCF（HL），则有∠BAE＝∠CBF，由此可证到∠AOB＝90°，然后在Rt△ABE中，运用面积法就可求出BO的长；当点F在AD上时，如图2②，易证Rt△ABE≌Rt△BAF（HL），则有∠BAE＝∠ABF，根据等角对等边可得OB＝OA，根据等角的余角相等可得∠AEB＝∠EBF，根据等角对等边可得OB＝OE，即可得到OA＝OB＝OE，只需求出AE的长就可解决问题．

（1）①如图1①，

∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，∠ABE＝∠C＝90°，

∴∠BAE+∠AEB＝90°，

∵BF⊥AE，

∴∠CBF+∠AEB＝90°，

∴∠BAE＝∠CBF，

在△ABE和△BCF中，

，

∴△ABE≌△BCF（ASA），

∴BF＝AE；

②OD＝AB．

证明：延长AD，交射线BM于点G，如图1②，

∵△ABE≌△BCF，

∴BE＝CF．

∵E为BC的中点，

∴CF＝BE＝BC＝DC，

∴CF＝DF．

∵DG∥BC，

∴∠DGF＝∠CBF．

在△DGF和△CBF中，

，

∴△DGF≌△CBF，

∴DG＝BC，

∴DG＝AD．

∵BF⊥AE，

∴OD＝AG＝AD＝AB；

（2）①若点F在CD上，如图2①，

在Rt△ABE和Rt△BCF中，

，

∴Rt△ABE≌Rt△BCF（HL），

∴∠BAE＝∠CBF，

∵∠BAE+∠AEB＝90°，

∴∠CBF+∠AEB＝90°，

∴∠AOB＝90°．

∵∠ABE＝90°，AB＝4，BE＝2，

∴AE＝＝2 ．

∵S△ABE＝ABBE＝AEBO，

∴BO＝．

②若点F在AD上，如图2②，

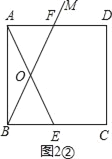
在Rt△ABE和Rt△BAF中，

，

∴Rt△ABE≌Rt△BAF（HL），

∴∠BAE＝∠ABF，

∴OB＝OA．

∵∠BAE+∠AEB＝90°，∠ABF+∠EBF＝90°，

∴∠AEB＝∠EBF，

∴OB＝OE，

∴OA＝OB＝OE．

∵∠ABE＝90°，AB＝4，BE＝2，

∴AE＝＝2，

∴OB＝AE＝．

综上所述：BO的长为或．