
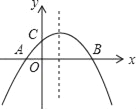
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣![]() .其中正确结论的序号是_____.
.其中正确结论的序号是_____.
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
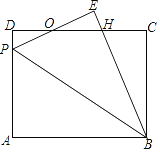
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=![]() n2+
n2+![]() n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),
如第1个三角形数N(1,3)=![]() ×12+
×12+![]() ×1=1;
×1=1;
第2个三角形数N(2,3)=![]() ×22+
×22+![]() ×2=3;
×2=3;
第3个四边形数N(3,4)=![]() ×32+
×32+![]() ×3=9;
×3=9;
第4个四边形数N(4,4)=![]() ×42+
×42+![]() ×4=16.
×4=16.
(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)
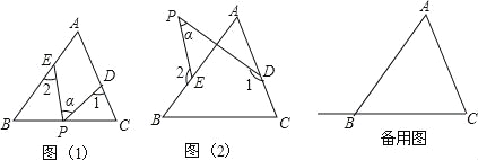
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置。如图所示,
现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系? ____________;
(3)连接CD、BD,则四边形ABDC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近______;(精确到0.1);
很大时,摸到白球的频率将会接近______;(精确到0.1);
(2)假如随机摸一次,摸到白球的概率P(白球)=______;
(3)试估算盒子里白色的球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
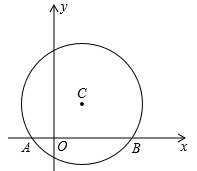
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com