
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)过点![]() 作与
作与![]() 轴平行的直线,交抛物线于点
轴平行的直线,交抛物线于点![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如图),点
(如图),点![]() ,
,![]() 分别为射线
分别为射线![]() 上的动点(点C、E都不与点B重合),连接AC、AE使得
上的动点(点C、E都不与点B重合),连接AC、AE使得![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
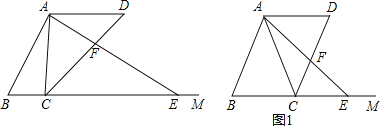
(1)如图1,当![]() 时,求AF的长.
时,求AF的长.
(2)当点![]() 在点
在点![]() 的右侧时,求
的右侧时,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.
(3)连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
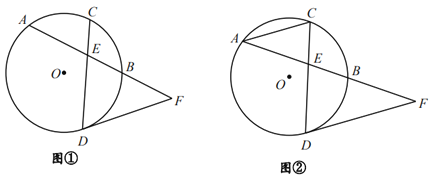
【题目】如图,已知,⊙O的半径![]() ,弦AB,CD交于点E,C为
,弦AB,CD交于点E,C为![]() 的中点,过D点的直线交AB延长线与点F,且DF=EF.
的中点,过D点的直线交AB延长线与点F,且DF=EF.
(1)如图①,试判断DF与⊙O的位置关系,并说明理由;
(2)如图②,连接AC,若AC∥DF,BE=![]() AE,求CE的长.
AE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
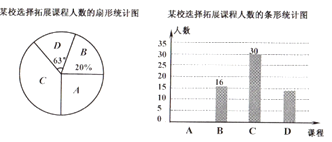
(1)求这次被调查的学生人数;
(2)请将条形统计图补充完整;
(3)假如全校有学生1000人,请估计选报“红船课程”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )

A.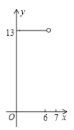 B.
B.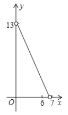 C.
C.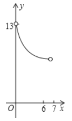 D.
D.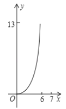
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上。甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地。两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示。
(分钟)之间的函数关系如图所示。
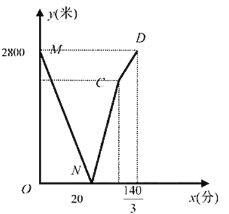
(1)当![]() ____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点
____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点![]() 的坐标为_____________;
的坐标为_____________;
(2)求出甲、乙两人相遇后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当乙到达距学校800米处时,求甲、乙两人之间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:无论函数解析式中自变量的字母系数取何值,函数的图象都会过某一个点,这个点称为定点. 例如,在函数![]() 中,当
中,当![]() 时,无论
时,无论![]() 取何值,函数值
取何值,函数值![]() ,所以这个函数的图象过定点
,所以这个函数的图象过定点![]() .
.
求解体验
(1)①关于![]() 的一次函数
的一次函数![]() 的图象过定点_________.
的图象过定点_________.
②关于![]() 的二次函数
的二次函数![]() 的图象过定点_________和_________.
的图象过定点_________和_________.
知识应用
(2)若过原点的两条直线![]() 、
、![]() 分别与二次函数
分别与二次函数![]() 交于点
交于点![]() 和点
和点![]() 且
且![]() ,试求直线
,试求直线![]() 所过的定点.
所过的定点.
拓展应用
(3)若直线![]() 与拋物线
与拋物线![]() 交于
交于![]() 、
、![]() 两点,试在拋物线
两点,试在拋物线![]() 上找一定点
上找一定点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有2个红球和2个白球,这些球除颜色外其余都相同,先从袋中摸出1个球后不放回,再摸出一个球.
(1)请用树状图或列表法列举出两次摸球可能出现的各种结果.
(2)求两次摸到不同颜色的球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com