
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+![]() :1,其中正确结论的序号为_________.
:1,其中正确结论的序号为_________.
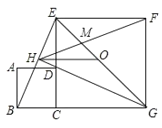
【答案】①②③
【解析】
证明△BCE≌△DCG,即可证得∠BEC=∠DGC,然后根据三角形的内角和定理证得∠EHG=90°,则HG⊥BE,然后证明△BGH≌△EGH,可得BG=EG,H是BE的中点,则OH是△BGE的中位线,根据三角形的中位线定理即可得到HO=![]() BG,HO∥BG,以及∠MOH=∠EGC=45°,再根据等腰直角三角形的性质,得出OF=
BG,HO∥BG,以及∠MOH=∠EGC=45°,再根据等腰直角三角形的性质,得出OF=![]() EG,∠OFG=45°,以及OH=OF,根据∠MHO+∠HOM=∠OFH+∠OFG,即可得出∠FMG=∠MFG,最后根据等腰直角三角形的边角关系,得出DB:AB=
EG,∠OFG=45°,以及OH=OF,根据∠MHO+∠HOM=∠OFH+∠OFG,即可得出∠FMG=∠MFG,最后根据等腰直角三角形的边角关系,得出DB:AB=![]() :1,即可得到DE:AB=
:1,即可得到DE:AB=![]() :1.
:1.
∵正方形ABCD的边CD在正方形ECGF的边CE上,
∴∠BCE=∠DCG=90°,BC=DC,EC=GC,
∴△BCE≌△DCG(SAS),
∴∠CGD=∠CEB,
又∵∠CDG=∠HDE,
∴∠EHD=∠GCD=90°,
∴GH⊥BE,故①正确;
∵∠EGC的平分线GH过点D,
∴∠BGH=∠EGH,
∵GH⊥BE,
∴∠BHG=∠EHG=90°,
∵GH=GH,
∴△BGH≌△EGH(ASA),
∴BG=EG,故②正确;
∵BG=EG,GH⊥BE,
∴H为BE的中点,
又∵O是EG的中点,
∴HO是△BEG的中位线,
∴HO=![]() BG,HO∥BG,
BG,HO∥BG,
∴∠MOH=∠EGC=45°,
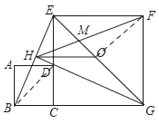
如图,连接FO,
∵O是EG的中点,
∴等腰Rt△EFG中,OF=![]() EG,∠OFG=45°,
EG,∠OFG=45°,
∴OH=OF,
∴∠OHF=∠OFH,
∴∠MHO+∠HOM=∠OFH+∠OFG,即∠FMG=∠MFG,
∴FG=MG,即△MFG是等腰三角形,故③正确;
如图,连接BD,
∵HG垂直平分BE,
∴DE=DB,
∵Rt△ABD中,DB:AB=![]() :1,
:1,
∴DE:AB=![]() :1,故④错误;
:1,故④错误;
故答案为:①②③


科目:初中数学 来源: 题型:
【题目】抛物线y1=ax2+c与x轴交于A、B两点,与y轴交于点C,点P在抛物线上,过P(1,﹣3),B(4,0)两点作直线y2=kx+b.
(1)求a、c的值;
(2)根据图象直接写出y1>y2时,x的取值范围;
(3)在抛物线上是否存在点M,使得S△ABP=5S△ABM,若存在,求出点M的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
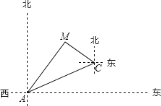
【题目】如图,某天然气公司的主输气管道从![]() 市向北偏东
市向北偏东![]() 方向直线延伸,测绘员在
方向直线延伸,测绘员在![]() 处测得要安装天然气的
处测得要安装天然气的![]() 小区在
小区在![]() 市北偏东
市北偏东![]() 方向,测绘员沿主输气管道步行
方向,测绘员沿主输气管道步行![]() 米到达
米到达![]() 处,测得小区
处,测得小区![]() 位于
位于![]() 的北偏西
的北偏西![]() 方向,请你在主输气管道上用尺规作图的方法(不写作法,保留作图痕迹)找出支管道连接点
方向,请你在主输气管道上用尺规作图的方法(不写作法,保留作图痕迹)找出支管道连接点![]() ,使到该小区铺设的管道最短,并求出
,使到该小区铺设的管道最短,并求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
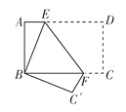
【题目】如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.

(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论,_____________.
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度![]() ,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
(3)将图1中的正方形CDEF,绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,得到如图3的情形,点
,得到如图3的情形,点![]() 恰好落在斜边
恰好落在斜边![]() 上,若
上,若![]() ,求正方形CDEF的边长.
,求正方形CDEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() 且
且![]() 于点E,与CD相交于点F,
于点E,与CD相交于点F,![]() 于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③
于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③![]() ;④AE=CF.其中正确的是____________(填序号)
;④AE=CF.其中正确的是____________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法一定正确的是( )
A.所有的等边三角形都是全等三角形
B.全等三角形是指形状相同的两个三角形
C.全等三角形是指面积相等的两个三角形
D.全等三角形的周长和面积分别相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com