
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
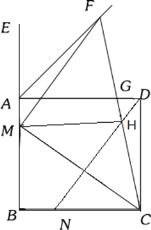
A.1B.2C.3D.4
【答案】D
【解析】
①设MC与DN交点是P,通过证明△MBC≌△NCD得到∠PNC=∠CMB,又证明则∠PNC +∠PCN =90°求出∠NPC=90°,则MC⊥ND,即可得到答案.
故①MC⊥ND正确.
②延长AE,作FQ⊥AF于点Q,利用勾股定理求出MC=5,再通过△MBC∽△FQM得到![]() 即
即![]() ,又因为QA=QF,则可以求得QA=QF =3,进而求得
,又因为QA=QF,则可以求得QA=QF =3,进而求得![]() ,在Rt△FMC中,利用勾股定理得
,在Rt△FMC中,利用勾股定理得![]() 则可以求得sin∠MFC的值.
则可以求得sin∠MFC的值.
③设(BM+DG)=AM+AG存在,利用边与边的关系可以求出DG,符合题意,即可求出答案.
④作HI⊥MF于点I,先证△CPN∽△CBM,求出PC,MP=MC-PC=5-![]() ,再通过证
,再通过证
四边形MPHI是矩形,求得IH= MP![]() ,知道△HMF的底和高,即可求出答案.
,知道△HMF的底和高,即可求出答案.
(1)

设MC与ND交于点P,如图所示.
∵四边形ABCD是正方形
∴CD=BC=AB=4
∠MBC=∠NCD=90°
∵AM=BN=1
∴NC=BC-BN=4-1=3
MB=AB-AM=4-1=3
∴NC=MB
在△MBC与△NCD中,
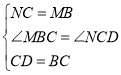
∴△MBC≌△NCD
∴∠PNC=∠CMB
∵∠MBC =90°
∴∠CMB+∠PCN =90°
则∠PNC +∠PCN =90°
∴∠NPC=180°-(∠PNC +∠PCN)=90°
∴MC⊥ND
故①MC⊥ND正确.
(2)
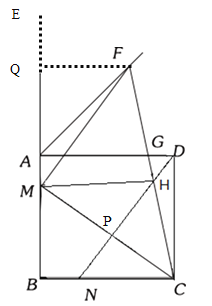
延长AE,作FQ⊥AF于点Q
∵MB=3,BC=4.∠B=90°
∴在Rt△MBC中,利用勾股定理得![]()
∠BCM+∠BMC =90°
∵MC⊥ND,MF∥ND
∴∠FMC=90°
∴∠QMF+∠BMC=180°-∠FMC=90°
∴∠QMF=∠BCM
∵FQ⊥AF
∠B=90°
∴∠FQM=∠B
∴△MBC∽△FQM
∴![]() 即
即![]()
∵四边形ABCD是正方形,AF平分∠QAG
∴∠QAF=![]()
又∵∠FQM=90°
∴∠QFA=∠QAF
∴QA=QF
∴![]() 变形为
变形为![]() 解得QA=QF =3
解得QA=QF =3
∴QM=QA+AM=4
∴在Rt△QMF中,利用勾股定理得![]()
∴在Rt△FMC中,利用勾股定理得![]()
∴sin∠MFC=![]() 故②正确
故②正确
(3)设(BM+DG)=AM+AG存在
由上述可知BM=3,AM=1,AG=AD-GD=4-DG,
将其代入(BM+DG)=AM+AG
得:(3+DG)=1+(4-DG)
解得DG=![]() ,符合题意,故③正确.
,符合题意,故③正确.
(4)
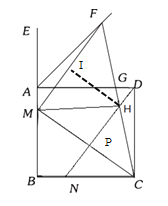
作HI⊥MF于点I
∵∠PCN=∠PCN,∠NPC=∠B=90°
∴△CPN∽△CBM
∴![]() 则
则![]() 即
即![]()
解得![]()
∴MP=MC-PC=5-![]()
∵∠IMP=∠MPH=∠MIH=90°
∴四边形MPHI是矩形
∴IH= MP![]()
∴S△HMF=![]() 故④正确
故④正确
综上所述四项全部正确,答案选D


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,连接PA、PC,PA=PC,∠APC=90°,把线段AP绕点A逆时针旋转120°,得到线段AQ(点P与点Q为对应点),连接BQ交AP于点E.点D为BQ的中点,连接AD、PD,若S△DAP=2,则AB=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
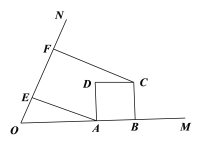
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
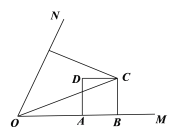
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
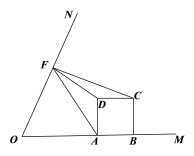
图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=![]() ,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
(1)当∠DCM=30°时,求DM的长度;
(2)如图2,延长BN、DC交于点E,求证:AM·DE=BE·CD;
(3)如图3,连接AN,则AM+AN的最小值是 .
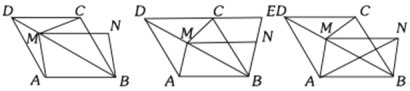
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大叔想用篱笆围成一个周长为80米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在![]() 轴,
轴,![]() 轴的正半轴上.函数
轴的正半轴上.函数![]() 的图象与CB交于点D,函数
的图象与CB交于点D,函数![]() (
(![]() 为常数,
为常数,![]() )的图象经过点D,与AB交于点E,与函数
)的图象经过点D,与AB交于点E,与函数![]() 的图象在第三象限内交于点F,连接AF、EF.
的图象在第三象限内交于点F,连接AF、EF.
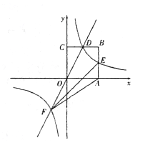
(1)求函数![]() 的表达式,并直接写出E、F两点的坐标.
的表达式,并直接写出E、F两点的坐标.
(2)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
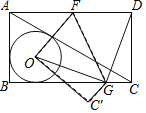
A.BC﹣AB=2B.AC=2ABC.AF=CDD.CD+DF=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com