
【题目】李大叔想用篱笆围成一个周长为80米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
【答案】(1)S=﹣x2+40x,0<x<40;(2)当x是20时,矩形场地面积S最大,最大面积是400.
【解析】
(1)由题目分析可知,矩形的另一边长应为![]() =40-x,由矩形的面积公式可以得出S与x之间的函数关系式;
=40-x,由矩形的面积公式可以得出S与x之间的函数关系式;
(2)根据二次函数的性质,以及x的取值范围,求出二次函数的最大值.
(1)由分析可得:S=x×(40﹣x)=﹣x2+40x,且有0<x<40,
所以S与x之间的函数关系式为:S=x×(40﹣x)=﹣x2+40x,自变量x的取值范围为:0<x<40;
(2)S=﹣x2+40x=﹣(x﹣20)2+400,
所以当x=20时,有S的最大值S=400,
答:当x是20时,矩形场地面积S最大,最大面积是400.


科目:初中数学 来源: 题型:
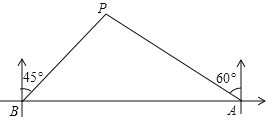
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
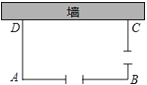
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
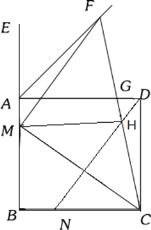
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示. 对于此抛物线有如下四个结论:
,其部分图象如图所示. 对于此抛物线有如下四个结论:
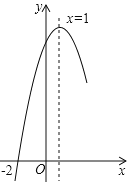
①![]() ;②
;②![]() ;
;
③若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点![]() 不在此抛物线上. 其中正确结论的序号是( )
不在此抛物线上. 其中正确结论的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC=DC,AC⊥DC,直线MN经过点A,作DB⊥MN,垂足为B,连接CB.
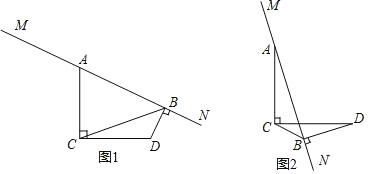
(1)直接写出∠D与∠MAC之间的数量关系;
(2)①如图1,猜想AB,BD与BC之间的数量关系,并说明理由;
②如图2,直接写出AB,BD与BC之间的数量关系;
(3)在MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,直接写出BC的值.
时,直接写出BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() ,直线
,直线![]()
(1)当m=0时,若直线![]() 经过此抛物线的顶点,求b的值
经过此抛物线的顶点,求b的值
(2)将此抛物线夹在![]() 之间的部分(含交点)图象记为
之间的部分(含交点)图象记为![]() ,若
,若![]() ,
,
①判断此抛物线的顶点是否在图象![]() 上,并说明理由;
上,并说明理由;
②图象![]() 上是否存在这样的两点:
上是否存在这样的两点:![]() ,其中
,其中![]() ?若存在,求相应的
?若存在,求相应的![]() 和
和![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
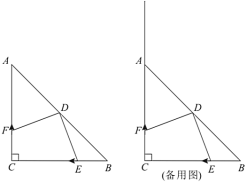
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com