
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
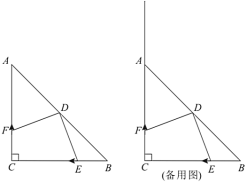
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
【答案】(1)8;(2)见解析;(3)![]() 或4或
或4或![]() 或
或![]() .
.
【解析】
(1)直接可求△ABC的面积;
(2)连接CD,根据等腰直角三角形的性质可求:∠A=∠B=∠ACD=∠DCB=45°,即BD=CD,且BE=CF,即可证△CDF≌△BDE,可得DE=DF;
(3)分△ADF的面积是△BDE的面积的两倍和△BDE与△ADF的面积的2倍两种情况讨论,根据题意列出方程可求x的值.
解:(1)∵S△ABC=![]()
![]() AC×BC
AC×BC
∴S△ABC=![]() ×4×4=8(cm2)
×4×4=8(cm2)
故答案为:8
(2)如图:连接CD
∵AC=BC,D是AB中点
∴CD平分∠ACB
又∵∠ACB=90°
∴∠A=∠B=∠ACD=∠DCB=45°
∴CD=BD
依题意得:BE=CF
∴在△CDF与△BDE中
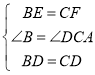
∴△CDF≌△BDE(SAS)
∴DE=DF
(3)如图:过点D作DM⊥BC于点M,DN⊥AC于点N,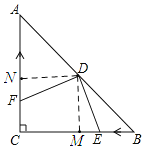
∵AD=BD,∠A=∠B=45°,∠AND=∠DMB=90°
∴△ADN≌△BDM(AAS)
∴DN=DM
若S△ADF=2S△BDE.
∴![]() ×AF×DN=2×
×AF×DN=2×![]() ×BE×DM
×BE×DM
∴|4-3x|=2x
∴x1=4,x2=![]()
若2S△ADF=S△BDE
∴2×![]() ×AF×DN=
×AF×DN=![]() ×BE×DM
×BE×DM
∴2×|4-3x|=x
∴x1=![]() ,x2=
,x2=![]()
综上所述:x=![]() 或4或
或4或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】嘉祥中学为加强现代信息技术教学,拟投资建一个初级计算机房和一个高级计算机房,每个计算机房只配置1台教师用机,若干台学生用机.其中初级机房教师用机每台8000元,学生用机每台3500元,高级机房教师用机每台11500元,学生用机每台7000元.已知两机房购买计算机的总钱数相等,且每个机房购买计算机的总钱数不少于20万元也不超过21万元.则该校拟建的初级机房,高级机房各应有多少台计算机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
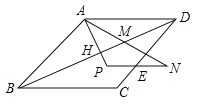
【题目】如图,E为菱形ABCD的边CD上任意点,将CE绕点E旋转一定角度后与AD平行.
(1)如图,若CE旋转后得到PE和NE,试判断下列结论是否成立?
①BD平分AN, ;
②BD⊥AP, (填写“成立”或“不成立”);
(2)证明(1)中你的判断.
(3)若∠ABC=60°,AB=BM=![]() +1,请直接写出CE的长度.
+1,请直接写出CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)用(m,n)表示小明取球时m与n的对应值,画出树状图(或列表),写出(m,n)的所有取值;
(2)求关于x的一元二次方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形EGFH是矩形.
小明继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
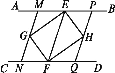
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____,MN∥EF,可得NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____,_____,故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com