
【题目】如图,P是等边三角形ABC内一点,连接PA、PC,PA=PC,∠APC=90°,把线段AP绕点A逆时针旋转120°,得到线段AQ(点P与点Q为对应点),连接BQ交AP于点E.点D为BQ的中点,连接AD、PD,若S△DAP=2,则AB=__.

【答案】4![]()
【解析】
延长QA到M,使得AM=AQ,连接BM,PM.首先证明△PAM是等边三角形,证明△MAB≌△PAC(SAS),推出∠AMB=∠APC=90°,由AQ=AM,BD=DQ,推出AD∥BM,BM=2AD,推出AD=![]() PA,再利用三角形的面积公式构建方方程求出PA即可解决问题.
PA,再利用三角形的面积公式构建方方程求出PA即可解决问题.
延长QA到M,使得AM=AQ,连接BM,PM.
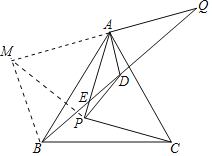
∵△ABC是等边三角形,
∴∠BAC=60°,
∵PA=PC,∠APC=90°,
∴∠PAC=∠PCA=45°,
∵∠PAQ=120°,
∴∠PAM=180°﹣120°=60°,
∵AM=AQ=AP,
∴△APM是等边三角形,
∴∠MAP=∠BAC=60°,
∴∠MAB=∠PAC,
∵AM=AP,AB=AC,
∴△MAB≌△PAC(SAS),
∴BM=PC,∠AMB=∠APC=90°,
∵AQ=AM,BD=DQ,
∴AD∥BM,BM=2AD,
∴AD=![]() PA,
PA,
∴∠QAD=∠QMB=90°,
∴∠PAD=∠MAD﹣∠MAP=90°﹣60°=30°,
∵S△PAD=2,
∴![]() PAADsin30°=2,
PAADsin30°=2,
∴![]() PA
PA![]() PA
PA![]() =2,
=2,
∴PA=4,
∴AB=AC=![]() PA=4
PA=4![]() ,
,
故答案为4![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
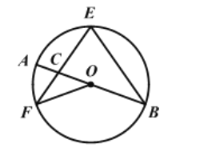
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
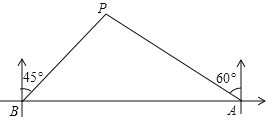
查看答案和解析>>
科目:初中数学 来源: 题型:
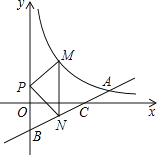
【题目】如图,已知直线y=![]() x+b与y轴交于点B(0,﹣3),与反比例函数y=
x+b与y轴交于点B(0,﹣3),与反比例函数y=![]() (x>0)的图象交于点A,与x轴交于点C,BC=3AC
(x>0)的图象交于点A,与x轴交于点C,BC=3AC
(1)求反比例函数的解析式;
(2)若P是y轴上一动点,M是直线AB上方的反比例函数y=![]() (x>0)的图象上一动点,直线MN⊥x轴交直线AB于点N,求△PMN面积的最大值.
(x>0)的图象上一动点,直线MN⊥x轴交直线AB于点N,求△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是⊙O的内接三角形,AB为直径,AC=BC,D、E是⊙O上两点,连接AD、DE、AE.

(1)如图1,求证:∠AED﹣∠CAD=45°;
(2)如图2,若DE⊥AB于点H,过点D作DG⊥AC于点G,过点E作EK⊥AD于点K,交AC于点F,求证:AF=2DG;
(3)如图3,在(2)的条件下,连接DF、CD,若∠CDF=∠GAD,DK=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
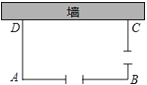
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
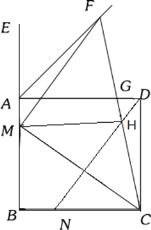
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com