
 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号)
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号) 分析 首先作CE⊥AB于E,依题意,AB=1464,∠EAC=30°,∠CBE=45°,设CD=x,则BE=x,进而利用正切函数的定义求出x即可.
解答  解:过点C作CE⊥AB的延长线于E,依题意得:AB=2000,∠EAC=30°,∠CBE=45°,
解:过点C作CE⊥AB的延长线于E,依题意得:AB=2000,∠EAC=30°,∠CBE=45°,
设CE=x,则BE=x,在Rt△ACE中,
tan30°=$\frac{CE}{AE}$=$\frac{x}{2000+x}$=$\frac{\sqrt{3}}{3}$,
即3x=2000$\sqrt{3}$+$\sqrt{3}$x,
解得:x=1000($\sqrt{3}$+1)=1000$\sqrt{3}$+1000,
∴1000$\sqrt{3}$+1000+600=(1600+1000$\sqrt{3}$)米
答:黑匣子C离海面约1600+1000$\sqrt{3}$米.
点评 此题主要考查了俯角的定义及其解直角三角形的应用,解题时首先正确理解俯角的定义,然后利用三角函数和已知条件构造方程解决问题.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
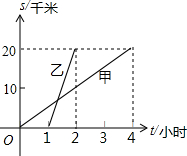 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )| A. | 甲的速度是4千米/小时 | B. | 乙的速度是10千米/小时 | ||
| C. | 甲比乙晚到B地3小时 | D. | 乙比甲晚出发1小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com