
 把一张长方形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=6,BC=8,则折痕EF的长为
把一张长方形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=6,BC=8,则折痕EF的长为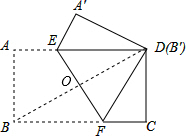 解:如图,连结BD.
解:如图,连结BD.| BC2+CD2 |
| 82+62 |
| BO |
| BC |
| OF |
| CD |
| 5 |
| 8 |
| OF |
| 6 |
| 15 |
| 4 |
| 15 |
| 2 |
| 15 |
| 2 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
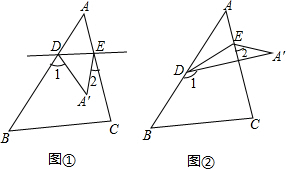
查看答案和解析>>
科目:初中数学 来源: 题型:
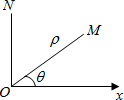 在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为
在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com