
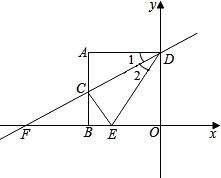
 如图,正方形ABOD的边长为2,C为AB的中点,直线CD交x轴于点F.
如图,正方形ABOD的边长为2,C为AB的中点,直线CD交x轴于点F.分析 (1)根据题意得出C、D的坐标,用待定系数法即可求出CD所在直线的解析式;
(2)过点C作CG⊥DE于G,先证明△CGD≌△CAD,得出CG=CA,GD=AD,再证明Rt△CBE≌Rt△CGE,得出BE=GE,设BE=GE=x,则OE=2-x,DE=2+x,根据勾股定理求出x,即可得出E的坐标;
(3)先证明CE⊥DF,延长EC交DA的延长线于E′,证出点E′为点E关于直线CD的对称点,DE′=2+$\frac{1}{2}$=$\frac{5}{2}$,得出E′坐标;连接OE′交直线CD于P,则点P即为使△POE的周长最小的点,根据勾股定理求出OE′,即可得出△POE周长的最小值;求出直线OE’的解析式,通过解方程组得出得P的坐标;
(4)分两种情况:①当点Q与点A重合时,∠CQD=90°,点Q的坐标为(-2,2);②作QM⊥OB于M,QN⊥ON于N,先证明△BQM≌△DQN,得出BQ=DQ,∠QBM=∠QDN,再证明CQ=BQ,即可得出结果.
解答 解(1)由题设得,C(-2,1),D(0,2),
设CD所在直线的解析式y=kx+b,
把C(-2,1),D(0,2)代入得:$\left\{\begin{array}{l}{-2k+b=1}\\{b=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴y=$\frac{1}{2}$x+2;
(2)过点C作CG⊥DE于G,如图1所示: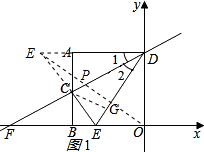
则∠CGD=90°,
∵四边形ABOD是正方形,
∴OB=AB=OD=AD=2,AD∥OB,∠CAD=∠CBE=∠DOE=∠ODA=90°,
在△CGD和△CAD中,
$\left\{\begin{array}{l}{∠2=∠1}&{\;}\\{∠CGD=∠CAD}&{\;}\\{CD=CD}&{\;}\end{array}\right.$,
∴△CGD≌△CAD(AAS),
∴CG=CA,GD=AD=2,
∵C为AB的中点,
∴CA=CB,
∴CB=CG,
在Rt△CBE和Rt△CGE中,
$\left\{\begin{array}{l}{CE=CE}\\{CB=CG}\end{array}\right.$,
∴Rt△CBE≌Rt△CGE(HL),
∴BE=GE,
设BE=GE=x,则OE=2-x,DE=2+x,
在Rt△DOE中,由勾股定理得,DE2=OE2+OD2,
即(2+x)2=(2-x)2+x2,
解得:x=$\frac{1}{2}$,
∴BE=$\frac{1}{2}$,OE=2-$\frac{1}{2}$=$\frac{3}{2}$,
即点E的坐标为(-$\frac{3}{2}$,0);
(3)由(1),(2)知:△CGD≌△CAD,△CBE≌△CGE,
∴∠ACD=∠GCD,∠GCE=∠BCE,
∵∠ACD+∠GCD+∠GCE+∠BCE=180°,
即2∠GCD+2∠GCE=180°,
∴∠GCD+∠GCE=90°,
∴CE⊥DF,
延长EC交DA的延长线于E′,如图1所示:
∵AD∥OB,CA=CB,
∴CE′=CE,AE′=BE=$\frac{1}{2}$,
则点E′为点E关于直线CD的对称点,DE′=2+$\frac{1}{2}$=$\frac{5}{2}$,
∴E′(-$\frac{5}{2}$,2);
连接OE′交直线CD于P,则点P即为使△POE的周长最小的点;
∴OE′=$\sqrt{(\frac{5}{2})^{2}+{2}^{2}}$=$\frac{\sqrt{41}}{2}$,
∴△POE周长的最小值为OE+OP+EP=OE+OP+PE’=OE+OE’=$\frac{3}{2}$+$\frac{\sqrt{41}}{2}$;
设直线OE’的解析式为y=ax,
将E′(-$\frac{5}{2}$,2)代入得:-$\frac{5}{2}$a=2,
解得:a=-$\frac{4}{5}$,
∴直线OE’的解析式为:y=-$\frac{4}{5}$x;
解方程组$\left\{\begin{array}{l}{y=-\frac{4}{5}x}\\{y=\frac{1}{2}x+2}\end{array}\right.$得:$\left\{\begin{array}{l}{x=-\frac{20}{13}}\\{y=\frac{16}{13}}\end{array}\right.$,
∴得P的坐标为(-$\frac{20}{13}$,$\frac{16}{13}$);
(4)在直线OA上存在点Q,使∠CQD=90°;
理由如下:分两种情况:①当点Q与点A重合时,∠CQD=90°,点Q的坐标为(-2,2);
②如图2所示:作QM⊥OB于M,QN⊥ON于N,连接BQ,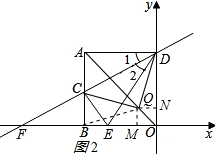 则QM=QN=ON=OM,
则QM=QN=ON=OM,
∴BM=DN,
在△BQM和△DQN中,
$\left\{\begin{array}{l}{QM=QN}&{\;}\\{∠QMB=∠QND=90°}&{\;}\\{BM=DN}&{\;}\end{array}\right.$,
∴△BQM≌△DQN(SAS),
∴BQ=DQ,∠QBM=∠QDN,
∴∠CBQ=∠ADQ,
∵∠CQD=∠DAC=90°,
∴A、C、Q、D四点共圆,
∴∠BCQ=∠ADQ,
∴∠CBQ=∠BCQ,
∴CQ=BQ,
∴Q在BC的垂直平分线上,
∴QM=QN=$\frac{1}{2}$CB=$\frac{1}{2}$,
∴Q的坐标为(-$\frac{1}{2}$,$\frac{1}{2}$);
综上所述:点Q的坐标为(-2,2),或(-$\frac{1}{2}$,$\frac{1}{2}$).
点评 本题是一次函数综合题,考查了正方形的性质、一次函数解析式的求法、全等三角形的判定与性质、勾股定理、最小值以及坐标特征等知识;本题难度较大,综合性强,特别是(2)(3)(4)中,需要通过作辅助线证明三角形全等、求一次函数解析式才能得出结果.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
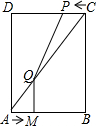 如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).
如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 18 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
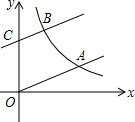 如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.
如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
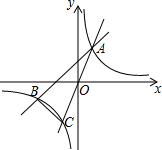 如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象交于点A,C,点A的坐标为(1,2),点B在反比例函数y=$\frac{m}{x}$(x<0)的图象上,且AB⊥BC.
如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象交于点A,C,点A的坐标为(1,2),点B在反比例函数y=$\frac{m}{x}$(x<0)的图象上,且AB⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
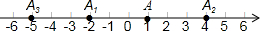 如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A4表示的数是7,如果点An与原点的距离不小于20,那么n的最小值是13.
如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A4表示的数是7,如果点An与原点的距离不小于20,那么n的最小值是13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
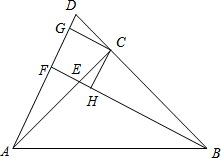 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com