
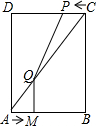
 如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).
如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).分析 (1)由QM∥CB,可得Rt△AQM∽Rt△ACB,根据相似三角形对应边成比例列出比例式,从而求出QM;
(2)由于∠DCA为锐角,故有两种情况:①当∠CPQ=90°时,点P为MQ延长线于CD的交点,可得AM+CP=CD,从而可求t;②当∠PQC=90°时,设点E为MQ延长线与CD的交点,容易证出Rt△PEQ∽Rt△QMA,再利用比例线段,结合EQ=EM-QM=4-2t,可求t.
解答 解:(1)∵在矩形ABCD中,∠B=90°,QM⊥AB于点M,
∴QM∥CB,
∴Rt△AQM∽Rt△ACB,
∴$\frac{QM}{CB}$=$\frac{AM}{AB}$,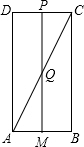 即$\frac{QM}{4}$=$\frac{t}{2}$,
即$\frac{QM}{4}$=$\frac{t}{2}$,
∴QM=2t=1;
(2)由于∠DCA为锐角,故有两种情况:
①当∠CPQ=90°时,点P为MQ延长线与CD的交点,
此时AM+CP=CD,即t+t=2,解得t=1,符合题意;
②当∠PQC=90°时,如图,设点E为MQ延长线与CD的交点,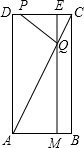 此时Rt△PEQ∽Rt△QMA,
此时Rt△PEQ∽Rt△QMA,
∴$\frac{EQ}{MA}$=$\frac{PE}{QM}$,
∵EQ=EM-QM=4-2t,
而PE=PC-CE=PC-(DC-DE)=t-(2-t)=2t-2,
∴$\frac{4-2t}{t}$=$\frac{2t-2}{2t}$,
∴t=$\frac{5}{3}$,符合题意;
综上所述,t=1或$\frac{5}{3}$.
点评 本题考查了一元二次方程的应用,利用了矩形的性质、相似三角形的判定和性质,还要掌握多种情况下的讨论解题法.


科目:初中数学 来源: 题型:解答题
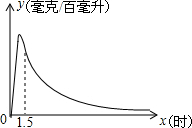 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
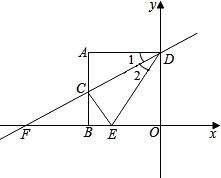 如图,正方形ABOD的边长为2,C为AB的中点,直线CD交x轴于点F.
如图,正方形ABOD的边长为2,C为AB的中点,直线CD交x轴于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com