
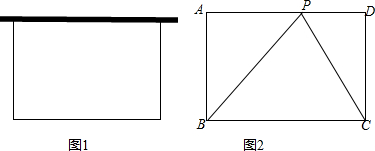
分析 (1)设这个矩形的长为x米(0<x≤12),则宽为$\frac{28-x}{2}$米,根据矩形的面积=长×宽,即可得出面积S关于长x之间的函数关系式,由二次函数在x的取值范围内的单调性即可得出结论;
(2)作点C关于AD的对称点C′,连接BC′交AD于点P,连接PC,由三角形中两边之和大于第三边可知,当B、P、C′共线时PB+PC最小,根据相似三角形的性质即可得出P点在AD中点时,用的绳子最短,求出此时C′B的长度即可;
(3)作一个圆,使该圆经过B、C点且和AD相切,由外角知识及圆周角定理可知∠BPC≤∠BGC(P、G重合时取等号),根据三角形的面积公式即可算出取最大值时sin∠BPC的值.
解答 解:(1)设这个矩形的长为x米(0<x≤12),则宽为$\frac{28-x}{2}$米,
根据矩形的面积公式可知S=x•$\frac{28-x}{2}$=-$\frac{1}{2}$(x-14)2+98,
∵0<x≤12,在此区间内面积S关于长x的函数单调递增,
∴当x=12时,S取最大值,S最大=96,
此时$\frac{28-x}{2}$=8.
故把整堵墙壁都用起来,矩形长为12米,宽为2米时矩形养鸡场的面积最大.
(2)作点C关于AD的对称点C′,连接BC′交AD于点P,连接PC,如图一所示.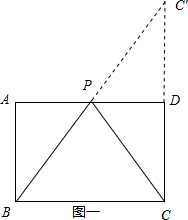
∵点C、C′关于AD对称,
∴PC=PC′,
∴PB+PC=PB+PC.
由三角形内两边之和大于第三边可知:当B、P、C′共线时PB+PC最小.
∵AD∥BC,
∴△C′PD∽△C′BC,
∴$\frac{PD}{BC}=\frac{C′D}{C′C}$=$\frac{1}{2}$,
∴PD=$\frac{1}{2}$BC,即P为AD的中点.
此时C′B=$\sqrt{B{C}^{2}+C′{C}^{2}}$=20(米).
故当点P选在AD中点处时,需要的绳子最短,最短绳长为20米.
(3)作一个圆,使该圆经过B、C点且和AD相切,如图二所示.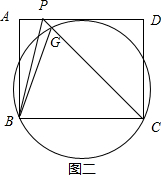
任取线段AD上一点P,连接BP、CP,令CP与圆交于点G,连接BG.
∵∠BGC=∠BPC+∠PBG,
∴∠BPC≤∠BGC.
当P、G两点重合时取等号,此时点P为AD的中点.
∵AD=12,AB=8,
∴AP=6,
由勾股定理得:BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=10,
∵△PBC的面积S=$\frac{1}{2}$BP•CP•sin∠BPC=$\frac{1}{2}$×10×10sin∠BPC=$\frac{1}{2}$BC•AB=$\frac{1}{2}$×12×8,
∴sin∠BPC=$\frac{24}{25}$.
故sin∠BPC的最大值为$\frac{24}{25}$.
点评 本题考查了二次函数的性质、最短路径问题、相似三角形的判定及性质、圆周角定理以及三角形的面积公式,解题的关键是:(1)根据面积=长×宽得出面积S关于长x的函数关系式;(2)找出当PB+PC最短时点P的位置;(3)找出∠BPC最大时点P的位置.本题属于中档题,(1)(2)难度不大;(3)寻找点P位置时有些难度,此问借助了圆周角定理以及外角的有关知识寻找到∠BPC最大时点P的位置,求∠BPC的正弦值时巧妙的利用了三角形的面积的两种求解方程,减少了解直角三角形的步骤.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
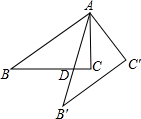 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com